REGRESSIONANALYSIS(y,x)
- is the set of dependent variables .
- is the set of independent variables.
Description
- This function is calculating the Regression analysis of the given data.
- This analysis is very useful for the analyzing the large amounts of data and making predictions.
- This analysis give the result in three table values.
- Regression statistics table.
- ANOVA table.
- Residual output.
1.Regression statistics :
- It contains multiple R, R Square, Adjusted R Square, Standard Error and observations.
- R square gives the fitness of the data with the regression line.
- That value is closer to 1 is the better the regression line fits the data.
- Standard Error refers to the estimated standard deviation of the error term. It is called the standard error of the regression.
2.ANOVA table:
- ANOVA is the analysis of variance.
- This table splits in to two components which is Residual and Regression.
Total sum of squares = Residual (error) sum of squares + Regression (explained) sum of squares.
- Also this table gives the probability, T stat, significance of F and P.
- When the significance of F is < 0.05, then the result for the given data is statistically significant.
- When the significance of F is > 0.05, then better to stop using this set of independent variables.
- Then remove a variable with a high P-value and return the regression until Significance F drops below 0.05.
- So the Significance of P value should be <0.05.
- This table containing the regression coefficient values also.
3.Residual output:
- The residuals show you how far away the actual data points are from the predicted data points.
Examples
1.
| A | B | |
|---|---|---|
| 1 | Temperature | Drying Time(Hrs) |
| 2 | 54 | 8 |
| 3 | 63 | 6 |
| 4 | 75 | 3 |
| 5 | 82 | 1 |
=REGRESSIONANALYSIS(A2:A5,B2:B5)
REGRESSION ANALYSIS OUTPUT
| Regression | Statistics |
|---|---|
| Multiple R | -0.9989241524588298 |
| R Square | 0.9978494623655915 |
| v14193 | 0.9967741935483871 |
| v15308 | 0.7071067811865362 |
| Source of Variation | Sum Of Squares | Degree Of Freedom | Mean Of Squares | F | Significance F |
|---|---|---|---|---|---|
| Regression: | 464 | 1 | 464 | 928 | 0.0010758475411702228 |
| Residual: | 1 | 2 | 0.5 | ||
| Total: | 465 | 3 |
| Coefficients | Standard Error | T Statistics | Probability | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intercept: | 86.5 | 0.6885767430246738 | 125.62143708199632 | 0.00006336233990811291 | 83.53729339698289 | 89.46270660301711 |
| X Variable | -4 | 0.13130643285972046 | -30.463092423456118 | 0.0010758475411701829 | -4.564965981777541 | -3.435034018222459 |
| Observation | Predicted Y | Residuals | Standard Residuals |
|---|---|---|---|
| 1 | 54.5 | -0.5 | -0.8660254037844387 |
| 2 | 62.5 | 0.5 | 0.8660254037844387 |
| 3 | 74.5 | 0.5 | 0.8660254037844387 |
| 4 | 82.5 | -0.5 | -0.8660254037844387 |
2.
| A | B | C | |
|---|---|---|---|
| 1 | Unit sales | Ads | population |
| 2 | 4000 | 12000 | 300000 |
| 3 | 5200 | 13150 | 411000 |
| 4 | 6800 | 14090 | 500000 |
| 5 | 8000 | 11900 | 650000 |
| 6 | 10000 | 15000 | 800000 |
- REGRESSIONANALYSIS(A1:A5,B1:C5)= NAN
See Also
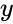 is the set of dependent variables .
is the set of dependent variables . is the set of independent variables.
is the set of independent variables.