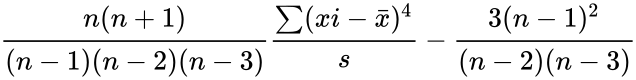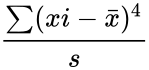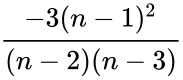Manuals/calci/tan

$wgFileExtensions[] = 'ogg';

TRIAL PAGE

For example TAN(1..100) can give an array of the results, which is the TAN value for each of the elements in the array. The array could be of any shape.

Failed to parse (syntax error): {\displaystyle f(x,r1,r2)=\Gamma[(r1+r2)/2](r1/r2)^r1/2*(x)r1/2-1/ Γ(r1/2)Γ(r2/2)(1+r1x/r2)^(r1+r2)/2, ==Description== <math>F(x,\lambda)=\begin{cases} 1-e^{-\lambda x} &, x \ge 0 \\ 0 &, x<0 \end{cases}}

Failed to parse (syntax error): {\displaystyle {\frac{n(n+1)}{(n-1)(n-2)(n-3)}*\frac{\sum{\frac{(xi-\bar{x})^4}{s}}\frac{-3(n-1)^2}{(n-2)(n-3)}}

${\frac {n(n+1)}{(n-1)(n-2)(n-3)}}{\frac {\sum (xi-{\bar {x}})^{4}}{s}}-{\frac {3(n-1)^{2}}{(n-2)(n-3)}}$

${\frac {\sum (xi-{\bar {x}})^{4}}{s}}$

${\frac {-3(n-1)^{2}}{(n-2)(n-3)}}$

Examples

1. Example 1

Spreadsheet

	A	B	C	D	E
1	2	3	7	9	15
2	8	12	13	20	25
3	14	3	9	6	15
4	12	23	1	42	17
5	11	20	9	78	25

From the above table values:

=MMULT(3,A1:A3)

15

21

24

=MMULT(6,A4:C4)

24

-30

54

1. Example 2

Matrix A

7	5
2	3
6	0
9	8

Matrix B

8	-4	11
2	7	5

• Here Matrix A is of order 4x2 and Matrix B is of order 2x3.
• So the Product Matrix is of order 4x3. i.e

1st Row 7*8+5*2 = 66  ;  7*(-4)+5*7 = 7  ;  7*11+5*5 = 102
2nd Row 2*8+3*2 = 22  ;  2*(-4)+3*7 = 13  ;  2*11+3*5 = 37 and so on

• =MMULT(B2:C5,D2:F3) gives

Result Matrix

66	7	102
22	13	37
48	-24	66
88	20	139

${\frac {{\binom {m}{x}}{\binom {N-M}{n-x}}}{\binom {m}{x}}}$

trial

Failed to parse (syntax error): {\displaystyle F(x,\mu,σ)=\frac{1}{2} \left[1+ erf \left (\frac{ln(x)-μ)}{σ\sqrt{2}}\right)\right ]= φ\left[\frac{ln(x)-μ}{σ}\right ]}

$F(x,\mu ,\sigma )={\frac {1}{2}}\left[1+erf\left({\frac {ln(x)-\mu )}{\sigma {\sqrt {2}}}}\right)\right]=\varphi \left[{\frac {ln(x)-\mu }{\sigma }}\right]$

\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}

Then |A|=a|e f -b|d f +c|d e

          h   i|       g    i|        g    h|

$a{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c{\begin{vmatrix}d&e\\g&h\end{vmatrix}}$

Trial 2

Failed to parse (syntax error): {\displaystyle f(x,r1,r2)=Γ[(r1+r2)/2](r1/r2)^{r1/2}*(x)^{r1/2-1}/ Γ(r1/2)Γ(r2/2)(1+r1x/r2)^(r1+r2)/2}

$f(x,r1,r2)={\frac {\Gamma [{\frac {r1+r2}{2}}]({\frac {r1}{r2}})^{\frac {r1}{2}}}{\Gamma ({\frac {r1}{2}})\Gamma ({\frac {r2}{2}})}}*{\frac {(x)^{{\frac {r1}{2}}-1}}{({\frac {1+r1x}{r2}})^{\frac {r1+r2}{2}}}}$

$f(x,r_{1},r_{2})={\frac {\Gamma [{\frac {r_{1}+r_{2}}{2}}]({\frac {r_{1}}{r_{2}}})^{\tfrac {r_{1}}{2}}}{\Gamma ({\frac {r_{1}}{2}})\Gamma ({\frac {r_{2}}{2}})}}*{\frac {(x)^{{\tfrac {r_{1}}{2}}-1}}{({\frac {1+r_{1}x}{r_{2}}})^{\tfrac {r_{1}+r_{2}}{2}}}}$

trial

1..10@DSIN

v11031	DSIN
1	0.01745240643728351
2	0.03489949670250097
3	0.05233595624294383
4	0.0697564737441253
5	0.08715574274765817
6	0.10452846326765346
7	0.12186934340514748
8	0.13917310096006544
9	0.15643446504023087
10	0.17364817766693033

TRIAL3

$s_{x1}.s_{x2}={\sqrt {{\frac {1}{2}}(s_{x1}^{2}+s_{x2}^{2})}}$

Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. TeX parse error: Double subscripts: use braces to clarify"): {\displaystyle s_{x}_{1}} $F(x,\alpha ,\beta )=1-e^{-}{({\frac {x}{\beta }})}^{\alpha }$

$P(x)={\begin{cases}0&for&x<a\\1/b-a&for&a<x<b\\0&for&x>b\end{cases}}$

$f(n)={\begin{cases}n/2,&{\mbox{if }}n{\mbox{ is even}}\\3n+1,&{\mbox{if }}n{\mbox{ is odd}}\end{cases}}$

${\begin{bmatrix}a_{11}&A_{21}^{T}\\A_{21}&A_{22}\end{bmatrix}}={\begin{bmatrix}l_{11}&0\\L_{21}&L_{22}\end{bmatrix}}{\begin{bmatrix}l_{11}&L_{21}^{T}\\0&L_{22}^{T}\end{bmatrix}}={\begin{bmatrix}l_{11}^{2}&L_{11}L_{21}^{T}\\L_{11}L_{21}&L_{21}L_{21}^{T}+L_{22}L_{22}^{T}\end{bmatrix}}$

Description

• This function gives the probability of the uniform distribution.
• Uniform distribution is a symmetric probability distribution.
• It is also called rectangular distribution.
• In $UNIFORMDISTRIBUTED(x,ll,ul)$ ,$x$ is the numeric value to find the probability of the distribution, $ll$ is the lower limit value and $ul$ is the upper limit value.
• The probability density function of the uniform distribution in the interval [a,b] are :

$P(x)={\begin{cases}0&for&x<a\\1/b-a&for&a<x<b\\0&for&x>b\end{cases}}$

Video

this is a test videos

this is a test videos

this is a test videos

9VZsMY15xeU

Video1

EmbedVideo does not recognize the video service "khanacademy".

Trial 5

$\left[{\frac {redemption}{\left(1+{\frac {yld}{frequency}}\right)^{\left(N-1+{\frac {DSC}{E}}\right)}}}\right]+\left[{\dfrac {100*{\frac {rate}{frequency}}*{\frac {DFC}{E}}}{\left(1+{\dfrac {yld}{frequency}}\right)^{\left({\dfrac {DSC}{E}}\right)}}}\right]+\left[\sum _{k=2}^{N}{\dfrac {100*{\frac {rate}{frequency}}}{\left(1+{\dfrac {yld}{frequency}}\right)^{\left(k-1+{\dfrac {DSC}{E}}\right)}}}\right]-\left[100*{\frac {rate}{frequency}}*{\frac {A}{E}}\right]$

Another Equation

$\left[{\frac {redemption}{\left(1+{\frac {yld}{frequency}}\right)^{\left(N+N_{3}+{\frac {DSC}{E}}\right)}}}\right]+\left[{\dfrac {100*{\frac {rate}{frequency}}*\sum _{i=1}^{NC}{\dfrac {DC_{i}}{NL_{i}}}}{\left(1+{\dfrac {yld}{frequency}}\right)^{\left(N_{3}+{\frac {DSC}{E}}\right)}}}\right]+\left[\sum _{k=1}^{N}{\dfrac {100*{\frac {rate}{frequency}}}{\left(1+{\dfrac {yld}{frequency}}\right)^{\left(k-N_{2}+{\dfrac {DSC}{E}}\right)}}}\right]-\left[100*{\frac {rate}{frequency}}*\sum _{i=1}^{NC}{\frac {A_{i}}{NL_{i}}}\right]$

Trial 6

$\left[{\dfrac {\left(redemption+\left(\left(\sum _{i=1}^{NC}{\frac {DC_{i}}{NL_{i}}}\right)*{\frac {100*rate}{frequency}}\right)\right)-\left(par+\left(\left(\sum _{i=1}^{NC}{\frac {A_{i}}{NL_{i}}}\right)*{\frac {100*rate}{frequency}}\right)\right)}{par+\left(\left(\sum _{i=1}^{NC}{\frac {A_{i}}{NL_{i}}}\right)*{\frac {100*rate}{frequency}}\right)}}\right]*\left[{\frac {frequency}{\left(\sum _{i=1}^{NC}{\frac {DSC_{i}}{NL_{i}}}\right)}}\right]$

$f(x,\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{\frac {-(x-\mu )^{2}}{2\sigma ^{2}}}$

Trial

$\int \limits _{1}^{3}{\frac {e^{3}/x}{x^{2}}}\,dx$

${\frac {1}{\Gamma (s)}}\int \limits _{0}^{\infty }{\frac {x^{s-1}}{e^{x-1}}}\,dx$

1	2	3	4
5 6 7 5 6 7
	0	0	0
5 6 7 5 6 7
	0	0	0

Trial New

5 6 7 5 6 7	0	0	0
0	5 6 7 5 6 7	0	0
1	0	5 6 7 5 6 7	0
0	0	0	5 6 7 5 6 7

Trail 6

${\begin{bmatrix}\alpha _{1}&{\alpha _{1}}^{q}&\cdots &{{\alpha _{1}}^{q}}^{n-1}\\\alpha _{2}&{\alpha _{2}}^{q}&\cdots &{{\alpha _{2}}^{q}}^{n-1}\\\alpha _{3}&{\alpha _{3}}^{q}&\cdots &{{\alpha _{3}}^{q}}^{n-1}\\\vdots &\vdots &\ddots &\vdots \\\alpha _{m}&{\alpha _{m}}^{q}&\cdots &{{\alpha _{m}}^{q}}^{n-1}\\\end{bmatrix}}$

• 2. MATRIX("permutation",18).$\$$_(SUM) = 18
• 3. MATRIX("permutation",5).$\$\$\$$(SUM)=
• 4. MATRIX("permutation",5).$\$\$$(SUM) =

Trail 7

Icon Name	Icon	Drawings
Update	Polygon	Polygon