LOGNORMDIST(number,mean,standarddeviation)
- is the value.
- is the mean value of ,
- is the standard deviation value of .
Description
- This function gives the value of the cumulative log normal distribution.
- This distribution is the continuous probability distribution.
- Lognomal distribution is also called Galton's distribution.
- A random variable which is log-normally distributed takes only positive real values.
- Suppose is Normally Distributed function, then also Normally Distributed
- also Normally Distributed.
- Let the Normal Distribution function and its Mean= , Standard Deviation =
- Then the lognormal cumulative distribution is calculated by:
where is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.
- And is the Cumulative Distribution function of the Standard Normal distribution.
- This function will give the result as error when
1. Any one of the argument is non-numeric. 2. Suppose or
ZOS
- The syntax is to calculate cumulative log normal distribution in ZOS is .
- is the value.
- is the mean value of .
- is the standard deviation value of .
- For e.g.,LOGNORMDIST(10,8.002,4.501)
Examples
- =LOGNORMDIST(2,5.4,2.76) = 0.044061652
- =LOGNORMDIST(10,24.05,12.95) = 0.046543186
- =LOGNORMDIST(50,87.0036,42.9784) = 0.026597569
- =LOGNORMDIST(-10,5,2) = NAN
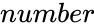 is the value.
is the value.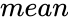 is the mean value of
is the mean value of 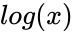 ,
,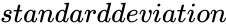 is the standard deviation value of
is the standard deviation value of