SERIESSUM(x,n,m,k)
- is the power series value.
- is the initial power value.
- is the step value to increase the n value for each term.
- is the set of coefficients by which each successive power of x is multiplied.
Description
- This function gives the value of the seriessum of the given set of values.
- Seriessum is defined by the following formula : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SERIESSUM(x,n,m,a)= a_1x^n + a_2x^{(n+m)} + a_3x^{(n+2m)} + … + a_jx^{(n+(j-1)m)} } .
- Here is the power-series value, is the starting power value, is the increasing value of a power and is the set of coefficients.
- According to the number of coefficients, the number of terms of the power series also get varies.
- For example there 5 values in coefficients, then 5 terms will be there in power series.
This function will give the result as error when any one of the argument is non-numeric.
Examples
- =SERIESSUM(3,2,2,{1,2,3,4,5,6}) = 3512493
- =SERIESSUM(1,0,4,{1,2,3}) = 6
- =SERIESSUM(2,1,5,{2,4,6,8}) = 536836
- =SERIESSUM(0,2,4,{1,2,3,4,5}) = 0
- =SERIESSUM(1,0,3,{1,2,3,4,5}) = 15
- =SERIESSUM(1,1,5,{1}) = 1
 is the power series value.
is the power series value. is the initial power value.
is the initial power value.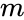 is the step value to increase the n value for each term.
is the step value to increase the n value for each term.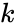 is the set of coefficients by which each successive power of x is multiplied.
is the set of coefficients by which each successive power of x is multiplied.