POISSONDISTRIBUTED(Numbers,Lambda)
- is the number of random numbers to display.
- is the mean value.
Description
- This function shows the random variables of Poisson distribution.
- It is a discrete frequency distribution which gives the probability of a number of independent events occurring in a fixed time.
- A Poisson random variable is the number of successes that result from a Poisson experiment.
- The probability distribution of a Poisson random variable is called a Poisson distribution.
- Suppose we conduct a Poisson experiment, in which the average number of successes within a given region is .
- Then, the Poisson probability is:
- where x is the actual number of successes that result from the experiment, and e is approximately equal to 2.71828.
- The Poisson distribution has the following properties:
- The mean of the distribution is equal to .
- The variance is also equal to .
- This function will give the result as error when b<0 and a value is not an integer.
Examples
- POISSONDISTRIBUTED(3,3) = 2 1 3
- POISSONDISTRIBUTED(5,45) = 37 39 45 35 47
- POISSONDISTRIBUTED(7,67.45) = 79.45 65.45 75.45 72.45 83.45 74.45 77.45
See Also
References
Poisson Probability Distribution
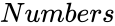 is the number of random numbers to display.
is the number of random numbers to display.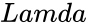 is the mean value.
is the mean value.