Manuals/calci/MAKECOMPLEXIMINUS
MAKECOMPLEXIMINUS(real,imaginary,suffix)
- is the real part of the complex number.
- is the imaginary part of the complex number.
- is the imaginary unit of the complex number.
Description
- MAKECOMPLEXIMINUS function converts the imaginary coefficient of a complex number into 'negative' coefficient.
- A complex number is a combination of a real and an imaginary number.
- A number which is positive or negative, rational or irrational or decimals are called real numbers.
- An Imaginary number is a number that when squring it gives a negative result.
- For e.g. . Because a negative times a negative is positive.
- A complex number is in the form , where and are real numbers and is the imaginary unit. Where
- To mention and , we must use the lower case only
- In a complex number real part is denoted by & imaginary part is denoted by .
- MAKECOMPLEXIMINUS returns the error value, when and are non-numeric.
- should be either or , otherwise it shows error value.
- A Complex number whose real part is zero is said to be purely imaginary.
- A Complex number whose imaginary part is zero is a real number. In that cases we have to assign '0' for that part.
- =MAKECOMPLEXIMINUS (5,2) gives
- =MAKECOMPLEXIMINUS (5,2,["j"]) gives
ZOS
- The syntax is to calculate MAKECOMPLEXIMINUS in ZOS is
- is the real part.
- is the imaginary part.
- is imaginary unit which is either "i" or "j".
Examples
- =MAKECOMPLEXIMINUS(4,5) = 4-i5
- =MAKECOMPLEXIMINUS(4,-5) = 4+i5
- =MAKECOMPLEXIMINUS(1,10,"j") = 1-j10
- =MAKECOMPLEXIMINUS(1,0) = 1+i0
- =MAKECOMPLEXIMINUS(1..3,5) = 1-i5 ; 2-i5; 3-i5
Related Videos
See Also
References
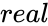 is the real part of the complex number.
is the real part of the complex number.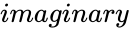 is the imaginary part of the complex number.
is the imaginary part of the complex number. is the imaginary unit of the complex number.
is the imaginary unit of the complex number.