Manuals/calci/MAKECOMPLEXIMINUSSIMPLE
MAKECOMPLEXIMINUSSIMPLE(imaginary)
- is the imaginary part of the complex number.
Description
- MAKECOMPLEXIMINUSSIMPLE function represents a complex number using the imaginary coefficient mentioned in the argument. Here the imaginary coefficient is converted to negative value.
- As the argument does not contain real number, the real number coefficient is considered zero.
- A complex number is a combination of a real and an imaginary number.
- A number which is positive or negative, rational or irrational or decimals are called real numbers.
- An Imaginary number is a number that when squring it gives a negative result.
- For e.g. . Because a negative times a negative is positive.
- A complex number is in the form , where and are real numbers and is the imaginary unit. Where
- To mention and , we must use the lower case only
- In a complex number real part is denoted by & imaginary part is denoted by .
- MAKECOMPLEXIMINUSSIMPLE returns the error value, when and are non-numeric.
- should be either or , otherwise it shows error value.
- A Complex number whose real part is zero is said to be purely imaginary.
- A Complex number whose imaginary part is zero is a real number. In that cases we have to assign '0' for that part.
- =MAKECOMPLEXIMINUSSIMPLE (8) gives
- =MAKECOMPLEXIMINUSSIMPLE (2,["j"]) gives
ZOS
- The syntax is to calculate MAKECOMPLEXIMINUS in ZOS is
- is the imaginary part.
Examples
- =MAKECOMPLEXIMINUSSIMPLE(5) = 4-i5
- =MAKECOMPLEXIMINUSSIMPLE(-5,["j") = 4+i5
- =MAKECOMPLEXIMINUSSIMPLE(1) = 1+i0
- =MAKECOMPLEXIMINUSSIMPLE(1..3) = 1-i5 ; 2-i5; 3-i5
Related Videos
See Also
References
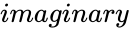 is the imaginary part of the complex number.
is the imaginary part of the complex number.