Manuals/calci/CHOLESKYFACTORIZATION
CHOLESKYFACTORIZATION(Matrix)
- is the array of numeric elements
Description
- This function gives the value of Cholesky factorization.
- It is called Cholesky Decomposition or Cholesky Factorization.
- In , is the set of values.
- The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices.
- Every positive definite matrix A can be factored as =
is lower triangular with positive diagonal elements is is the conjugate transpose value of
- Every Hermitian positive-definite matrix has a unique Cholesky decomposition.
- Here , is set of values to find the factorization value.
- Partition matrices in = is
Algorithm
- Determine and = =
- Compute from =
- this is a Cholesky Factorization of order
- If the matrix A is Hermitian and positive semi-definite, then it still has a decomposition of the form A = LL^T if the diagonal entries of L are allowed to be zero.
- Also A can be written as LL^T for some invertible L, lower triangular or otherwise, then A is Hermitian and positive definite.
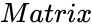 is the array of numeric elements
is the array of numeric elements