SKEWSYMMETRIC(Order)
- is the order of the skew symmetric matrix.
Description
- This function shows the Skew Symmetric matrix with the given order.
- Skew Symmetric is also called Anti Symmetric or Antimetric.
- A Skew Symmetric is a square matrix which satisfies the following identity ,where is the matrix transpose.
- If the entry in the row and column is .
- i.e. then the skew symmetric condition is = .
- So its diagonal values are "0".
Examples
1. SKEWSYMMETRIC(4)
| 0 | -39 | 2 | 25 |
| 39 | 0 | 15 | 72 |
| (-2) | -15 | 0 | 43 |
| (-25) | -72 | -43 | 0 |
2. SKEWSYMMETRIC(9)
| 0 | 48 | -36 | 72 | 25 | 51 | -13 | -98 | 70 |
| (-48) | 0 | -97 | -33 | 78 | -30 | -56 | 62 | 45 |
| 36 | 97 | 0 | 42 | -47 | 58 | 94 | 24 | -43 |
| (-72) | 33 | -42 | 0 | -23 | -77 | -80 | 69 | 70 |
| (-25) | -78 | 47 | 23 | 0 | -17 | 17 | -100 | 34 |
| (-51) | 30 | -58 | 77 | 17 | 0 | -43 | -67 | 0 |
| 13 | 56 | -94 | 80 | -17 | 43 | 0 | -24 | 55 |
| 98 | -62 | -24 | -69 | 100 | 67 | 24 | 0 | 76 |
| (-70) | -45 | 43 | -70 | -34 | 0 | -55 | -76 | 0 |
See Also
References
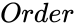 is the order of the skew symmetric matrix.
is the order of the skew symmetric matrix.