Manuals/calci/KURT
KURT(n1,n2,…)
- , are values to calculate kurtosis.
Description
- This function gives the value of Kurtosis of a given set.
- Kurtosis is the peak or flatness of a frequency distribution graph especially with respect to the concentration of values near the Mean as compared with the Normal Distribution.
- A normal distribution has a Kurtosis of 3.
- Distributions having higher Kurtosis have flatter tails or more extreme values that phenomenon called 'leptokurtosis' also it is the positive excess Kurtosis , and those with lower Kurtosis have fatter middles or fewer extreme value that phenomenon called 'Platykurtosis' also it is the negative excess Kurtosis.
- Example for positive Kurtosis(leptokurtosis) is Exponential distribution, Poisson distribution, Laplace Distribution.
- Example for Negative Kurtosis(platykurtosis) is Bernoulli distribution, Uniform distribution.
- Kurtosis has no units.
- Kurtosis is defined by:
- Kurtosis=:
Failed to parse (syntax error): {\displaystyle {\frac{n(n+1)}{(n-1)(n-2)(n-3)}*\frac{\sum{\frac{(xi-\bar{x})^4}{s}}\frac{-3(n-1)^2}{(n-2)(n-3)}} , where is the sample standard deviation.x(bar) is the arithmetic mean.
- In this function arguments may be any type like numbers,names,arrays or references that contain numbers.
- We can give logical values and text references also directly.
- Suppose the referred argument contains any null cells, logical values like that values are not considered.
- This function will return the result as error when
- Any one of the argument is non-numeric.
- suppose the number of data points are less than four or the standard deviation of the sample is zero
- The referred arguments could not convert
in to numbers.
Examples
1.DATA 14 11 23 54 38 KURT(C1:C5)=-0.8704870492 2. DATA={6,7,8,9,10} KURT(A1:A5)=-1.199999999 3.DATA={1898,1987,1786,1947} KURT(B1:B4)=0.870901113729 4.DATA={26,16,12} KURT(D1:D3)=NAN
 ,
,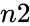 are values to calculate kurtosis.
are values to calculate kurtosis.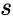 is the sample standard deviation.x(bar) is the arithmetic mean.
is the sample standard deviation.x(bar) is the arithmetic mean.