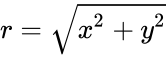Manuals/calci/IMSQRT
IMSQRT(z)
- is the complex number is of the form
Description
- This function gives square root of a complex number.
- IMSQRT(z), Where z is the complex number is in the form of "x+iy".
- where x&y are the real numbers.'i' imaginary unit ..
- The square root of a complex number is defined by Failed to parse (syntax error): {\displaystyle \sqrt{z}=\sqrt{x+iy}=\sqrt{r.e^iθ}=\sqrt{r}(cos(θ/2)+isin(θ/2)}
- where r is the modulus of z.
- And θ is the argument of z. Failed to parse (syntax error): {\displaystyle θ=tan^{-1}(y/x)} also θ∈(-Pi(),Pi()].
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
=IMSQRT("2+3i")=1.67414922803554+0.895977476129838i =IMSQRT("-4-5i")=1.09615788950152-2.2806933416653i =IMSQRT("7")=2.64575131106459 =IMSQRT("8i")=2+2i
''''''' ''''
Description
This function calculates the square root of a complex number in a + bi or a + bj text format.
IMSQRT
The square root of a complex number is:
IMSQRT(IN)
where IN is the complex number
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 1.455346690225355+0.34356074972251243i | |||
| Row2 | ||||
| Row3 | ||||
| Row4 | ||||
| Row5 | ||||
| Row6 |
Let's see an example
I.e =IMSQRT(“2+i”) is 1.4553+0.34356i
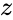 is the complex number is of the form
is the complex number is of the form 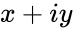
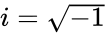 .
.