Manuals/calci/KRUSKALWALLISTEST
KRUSKALWALLISTEST(Array,Confidencelevel,Logicalvalue)
- is the set of values to find the test statistic.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the test statistic value of the Kruskal Wallis test.
- It is one type of Non parametric test.
- It is a logical extension of the Wilcoxon-Mann-Whitney Test.
- The parametric equivalent of the Kruskal-Wallis test is the one-way analysis of variance (ANOVA).
- This test is used for comparing more than two sample that are independent or not related.
- It is used to test the null hypothesis that all populations have identical distribution functions against the alternative hypothesis that at least two of the samples differ only with respect to Median.
- Kruskal–Wallis is also used when the examined groups are of unequal size.
- When the Kruskal-Wallis test leads to significant results, then at least one of the samples is different from the other samples.
- The test does not identify where the differences occur or how many differences actually occur.
- Since it is a non-parametric method, the Kruskal–Wallis test does not assume a normal distribution of the residuals, unlike the analogous one-way analysis of variance.
- However, the test does assume an identically shaped and scaled distribution for each group, except for any difference in medians.
- The Kruskal Wallis test data are having the following properties:
- 1.The data points must be independent from each other.
- 2.The distributions do not have to be normal and the variances do not have to be equal.
- 3.The data points must be more than five per sample.
- 4.All individuals must be selected at random from the population.
- 5.All individuals must have equal chance of being selected.
- 6.Sample sizes should be as equal as possible but some differences are allowed.
- Steps for Kruskal Wallis Test:
- 1. Define Null and Alternative Hypotheses:
- Null Hypotheses:There is no difference between the conditions.
- Alternative Hypotheses:There is a difference between the conditions.
- 2.State Alpha:Alpha=0.05.
- 3.Calculate degrees of freedom:df = k – 1, where k = number of groups.
- 4.State Decision Rule:From the Chi squared table calculate the critical value.
- Suppose the is greater than the critical value then reject the null hypothesis
- 5.Calculate the Test Statistic:
- 6.State Results:In this step we have to take a decision of null hypothesis either accept or reject depending on the critical value table.
- 7.State Conclusion:To be significant, our obtained H has to be equal to or LESS than this critical value.
Example
| Method1 | Method2 | Method3 |
| 94 | 82 | 89 |
| 87 | 85 | 68 |
| 90 | 79 | 72 |
| 74 | 84 | 76 |
| 86 | 61 | 69 |
| 97 | 72 | 65 |
| 0 | 80 | 0 |
- =LEVENESTEST(B1:C5,.05,0)
| Method1 | Method2 | Method3 |
| 18 | 11 | 16 |
| 15 | 13 | 3 |
| 17 | 9 | 5.5 |
| 7 | 12 | 8 |
| 14 | 1 | 4 |
| 19 | 5.5 | 2 |
| 10 |
| Method1 | Method2 | Method3 | |
| Sum of Ranks | 90 | 61.5 | 38.5 |
| Group Size | 6 | 7 | 6 |
| R^2/n | 1350 | 540.3214285714286 | 247.04166666666666 |
| TotalRankSum | 190 | ||
| Total Group Size | 19 | ||
| Total R^2/n | 2137.363095238095 | ||
| H | 7.495676691729315 | ||
| df | 2 | ||
| p-value | 0.023568638074462633 | ||
| a | 0.05 |
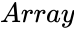 is the set of values to find the test statistic.
is the set of values to find the test statistic.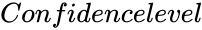 is the value between 0 and 1.
is the value between 0 and 1.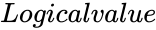 is either TRUE or FALSE.
is either TRUE or FALSE.