Manuals/calci/SVD
Jump to navigation
Jump to search
SVD(Matrix)
- is the set of values.
Description
- The singular value decomposition of a matrix A is the factorization of A into the product of three matrices
- Where the columns of U and V are orthonormal and the matrix S is diagonal with positive real entries
- Singular value decomposition is defined for all matrices (rectangular or square).
- The rank of a matrix is equal to the number of non-zero singular values.
Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers.
- Then there exists a factorization, called a singular value decomposition of A, of the form
where U is an m × m unitary matrix, S is a diagonal m × n matrix with non-negative real numbers on the diagonal, V is an n × n unitary matrix over K, and is the conjugate transpose of V.
Example
| A | B | C | |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | -1 | -2 | 0 |
| 3 | 0 | 1 | -1 |
=SVD(A1:C3)
0.12000026038175768 -0.8097122815927454 -0.5744266346072238 |
-0.9017526469088556 0.15312282248412068 -0.40422217285469236 |
0.41526148545366265 0.5664975042066532 -0.7117854145923829 |
2.4605048700187635 0 0 |
0 1.699628148275319 0 |
0 0 0.23912327825655444 |
0.4152614854539272 -0.566497504206459 -0.711854145923831 |
0.9017526469087841 0.15312282248454143 0.4042221728546923 |
-0.12000026038137995 -0.8097122815928015 0.5744266346072238 |
| A | B | C | |
|---|---|---|---|
| 1 | 1 | 2 | 3 |
| 2 | 4 | 5 | 6 |
| 3 | 7 | 8 | 9 |
=SVD(A1:C3)
 is the set of values.
is the set of values.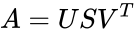
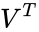 is the conjugate transpose of V.
is the conjugate transpose of V.