Difference between revisions of "Manuals/calci/ADJ"
Jump to navigation
Jump to search
| Line 56: | Line 56: | ||
\end{vmatrix} \\ | \end{vmatrix} \\ | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
| − | + | ||
| − | + | ==Examples== | |
| − | + | 1.adj([[10,12],[-14,21]]) | |
| − | + | {| class="wikitable" | |
| + | |+Spreadsheet | ||
| + | |- | ||
| + | | 21 ||-12 | ||
| + | |- | ||
| + | |14 || 10 | ||
| + | |} | ||
| + | 2.adj([[4,5,8],[3,-6,-9],[10,-12,4]]) | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | | -132 ||-116||2.9999999999999982 | ||
| + | |- | ||
| + | | -102|| -64|| 60 | ||
| + | |- | ||
| + | | 24 || 98 || -39 | ||
| + | |} | ||
| + | |||
| + | 3.adj([[5,-2,2,7],[1,0,0,3], [-3,1,5,0], [3,-1,-9,4]]) | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | | -12 ||76||-60 ||-36 | ||
| + | |- | ||
| + | | -56 || 207.99999999999997 || -81.99999999999999 || -57.99999999999999 || | ||
| + | |- | ||
| + | | 4 || 3.999999999999999 || -1.9999999999999998 || -10 || | ||
| + | |- | ||
| + | | 4 ||3.9999999999999982 || 20 || 12 || | ||
| + | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/MATRIXADJOINT | MATRIXADJOINT ]] | ||
| + | *[[Manuals/calci/MINVERSE | MINVERSE ]] | ||
| + | *[[Manuals/calci/MMULT | MMULT ]] | ||
==References== | ==References== | ||
*[https://en.wikipedia.org/wiki/Adjugate_matrix Adjugate matrix] | *[https://en.wikipedia.org/wiki/Adjugate_matrix Adjugate matrix] | ||
Revision as of 15:05, 1 June 2017
ADJ(Array)
- is the set of values.
Description
- This function shows the Adjoint of a given matrix.
- In , is the set of matrix values.
- Adjoint of a matrix is called adjugate, classical adjoint, or adjunct.Adjoint of a matrix formed by taking the transpose of the cofactor matrix of a given original Square matrix.
- Adjoint of matrix A is written by .
- The adjugate of A is the transpose of the cofactor matrix C of A, .
- Also adjoint of a matrix is defined by .
- The adjugate of 1x1 matrix is .
- The adjugate of 2x2 matrix is .
- Consider3x3 matrix .
- Its adjugate is the transpose of its cofactor matrix:
Examples
1.adj([[10,12],[-14,21]])
| 21 | -12 |
| 14 | 10 |
2.adj([[4,5,8],[3,-6,-9],[10,-12,4]])
| -132 | -116 | 2.9999999999999982 |
| -102 | -64 | 60 |
| 24 | 98 | -39 |
3.adj([[5,-2,2,7],[1,0,0,3], [-3,1,5,0], [3,-1,-9,4]])
| -12 | 76 | -60 | -36 | |
| -56 | 207.99999999999997 | -81.99999999999999 | -57.99999999999999 | |
| 4 | 3.999999999999999 | -1.9999999999999998 | -10 | |
| 4 | 3.9999999999999982 | 20 | 12 |
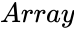 is the set of values.
is the set of values.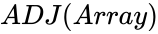 ,
,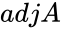 .
.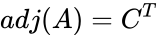 .
.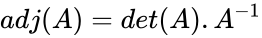 .
. .
.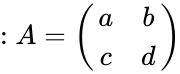 is
is 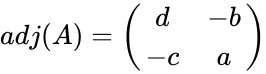 .
. .
.