Difference between revisions of "Manuals/calci/BINOMIALCOEFFICIENT"
Jump to navigation
Jump to search
| Line 41: | Line 41: | ||
| − | [[Z_API_Functions | List of Main Z Functions]] | + | *[[Z_API_Functions | List of Main Z Functions]] |
| − | [[ Z3 | Z3 home ]] | + | *[[ Z3 | Z3 home ]] |
Revision as of 00:58, 13 March 2017
BINOMIAL(n,k)
- is the number of items.
- is the number of selection.
Description
- This function gives the coefficent of the binomial distribution.
- Binomial coefficient is the set of positive integer which equals the number of combinations of k items that can be selected from a set of n items.
- The coefficients satisfy the Pascals recurrence.
- The binomial coefficents are denoted by and it is read by n choose k.
- It is the coefficient of the term in the polynomial expansion of the binomial thorem .
- The coefficient is occur in the formula of binomial thorem:
where .
- To find the coefficient of the binomial ,we can use several methods.
1. Recursive formula 2. Multiplicative formula 3. Factorial formula.
- 1.Recursive Formula:
for and .
- 2. Multiplicative formula:
- 3.Factorial formula:
where ,and which is zero when .
- Also for the initial values for .
- Most compact formula for the coefficient of the binomial value is Factorial formula.
- Factorial formula is symmetric of the combination formula.
Examples
- =BINOMIAL(10,3)= 120
- =BINOMIAL(32,0)= 1
- =BINOMIAL(10,7) = 120
See Also
References
 is the number of items.
is the number of items.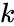 is the number of selection.
is the number of selection.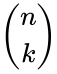 and it is read by n choose k.
and it is read by n choose k.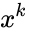 term in the polynomial expansion of the binomial thorem
term in the polynomial expansion of the binomial thorem 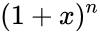 .
.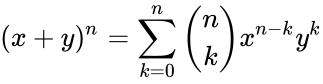 where
where 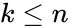 .
.
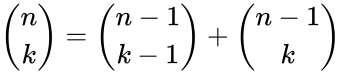 for
for 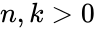 and
and  .
.
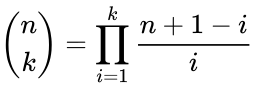
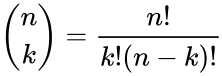 where
where 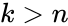 .
.
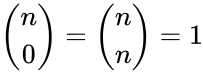 for
for 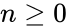 .
.