Difference between revisions of "Manuals/calci/CHOLESKY"
Jump to navigation
Jump to search
| (30 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size: | + | <div style="font-size:25px">'''CHOLESKY (Matrix) '''</div><br/> |
| − | *<math> | + | *<math>Matrix</math> is the array of numeric elements. |
==Description== | ==Description== | ||
| Line 7: | Line 7: | ||
*The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices. | *The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices. | ||
*Every positive definite matrix A can be factored as <math>A</math> = <math>LL^{T}</math> | *Every positive definite matrix A can be factored as <math>A</math> = <math>LL^{T}</math> | ||
| − | |||
<math>L</math> is lower triangular with positive diagonal elements | <math>L</math> is lower triangular with positive diagonal elements | ||
<math>L^{T}</math> is is the conjugate transpose value of <math>L</math> | <math>L^{T}</math> is is the conjugate transpose value of <math>L</math> | ||
| − | *Every Hermitian positive-definite matrix | + | *Every Hermitian positive-definite matrix has a unique Cholesky decomposition. |
| − | *Here <math>CHOLESKY( | + | *Here <math>CHOLESKY (Matrix) </math>, <math>Matrix</math> is set of values to find the factorization value. |
| − | *Partition matrices in | + | *Partition matrices in <math>A</math> = <math>LL^{T}</math> is |
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | a_{11} & A_{21}^{T}\\ | ||
| + | A_{21} & A_{22} | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | l_{11} & 0\\ | ||
| + | L_{21} & L_{22} | ||
| + | \end{bmatrix} | ||
| − | == | + | \begin{bmatrix} |
| + | l_{11} & L_{21}^{T}\\ | ||
| + | 0 & L_{22}^{T} | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | l_{11}^{2} & L_{11}L_{21}^{T}\\ | ||
| + | L_{11}L_{21} & L_{21}L_{21}^{T} + L_{22}L_{22}^{T} | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |||
| + | :<h2>Algorithm</h2> | ||
| + | <ol> | ||
| + | <li>Determine <math>l_{11}</math> and <math>L_{21}</math></li> | ||
| + | <math>l_{11}</math> = <math>\sqrt{a_{11}}</math> | ||
| + | <math>L_{21}</math> = <math>\frac{1}{l_{11}}A_{21}</math> | ||
| + | <li>Compute <math>L_{22}</math> from </li> | ||
| + | <math>A_{22}-L_{21}L_{21}^{T}</math> = <math>L_{22}L_{22}^{T}</math> | ||
| + | *This is a Cholesky Factorization of order <math>n-1</math> | ||
| + | </ol> | ||
==Examples== | ==Examples== | ||
| − | + | {| class="wikitable" | |
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 16 || 32 || 12 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 12 || 18 || 0 | ||
| + | |- | ||
| + | ! 3 | ||
| + | | -5 || 0 || 11 | ||
| + | |} | ||
| + | =CHOLESKY(A1:C3) | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|+Result | |+Result | ||
|- | |- | ||
| Line 30: | Line 71: | ||
|} | |} | ||
| − | + | {| class="wikitable" | |
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 25 || 15 || -5 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 15 || 18 || 0 | ||
| + | |- | ||
| + | ! 3 | ||
| + | | -5 || 0 || 11 | ||
| + | |} | ||
| + | =CHOLESKY(A1:C3) | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 41: | Line 96: | ||
| -1 || 1 || 3 | | -1 || 1 || 3 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=gFaOa4M12KU|280|center|Cholesky Decomposition}} | ||
==See Also== | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/PASCAL| PASCAL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://www.seas.ucla.edu/~vandenbe/103/lectures/chol.pdf Cholesky Factorization] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:55, 26 November 2018
CHOLESKY (Matrix)
- is the array of numeric elements.
Description
- This function gives the value of Cholesky factorization.
- It is called Cholesky Decomposition or Cholesky Factorization.
- The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices.
- Every positive definite matrix A can be factored as =
is lower triangular with positive diagonal elements is is the conjugate transpose value of
- Every Hermitian positive-definite matrix has a unique Cholesky decomposition.
- Here , is set of values to find the factorization value.
- Partition matrices in = is
Algorithm
- Determine and = =
- Compute from =
- This is a Cholesky Factorization of order
Examples
| A | B | C | |
|---|---|---|---|
| 1 | 16 | 32 | 12 |
| 2 | 12 | 18 | 0 |
| 3 | -5 | 0 | 11 |
=CHOLESKY(A1:C3)
| 4 | 0 | 0 |
| 3 | 3 | 0 |
| -1.25 | 1.25 | 2.80624 |
| A | B | C | |
|---|---|---|---|
| 1 | 25 | 15 | -5 |
| 2 | 15 | 18 | 0 |
| 3 | -5 | 0 | 11 |
=CHOLESKY(A1:C3)
| 5 | 0 | 0 |
| 3 | 3 | 0 |
| -1 | 1 | 3 |
Related Videos
See Also
References
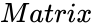 is the array of numeric elements.
is the array of numeric elements. =
= 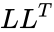
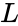 is lower triangular with positive diagonal elements
is lower triangular with positive diagonal elements
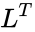 is is the conjugate transpose value of
is is the conjugate transpose value of 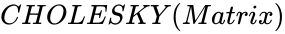 ,
, 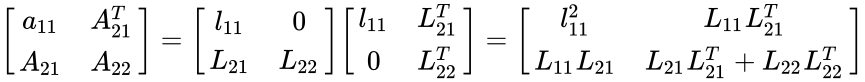
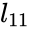 and
and 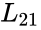

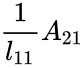
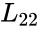 from
from  =
= 
