Difference between revisions of "Manuals/calci/FDIST"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*This distribution is the ratio of two chi-square distributions with degrees of freedom r1 and r2, respectively, where each chi-square has first been divided by its degrees of freedom. | *This distribution is the ratio of two chi-square distributions with degrees of freedom r1 and r2, respectively, where each chi-square has first been divided by its degrees of freedom. | ||
*The Probability density function of the F distribution is: | *The Probability density function of the F distribution is: | ||
| − | <math>f(x, | + | <math>f(x,r_1,r_2)=\frac{\Gamma[\frac{r_1+r_2}{2}](\frac{r_1}{r_2})^{\tfrac{r_1}{2}}}{ \Gamma(\frac{r_1}{2})\Gamma(\frac{r_2}{2})}*\frac{(x)^{\tfrac{r_1}{2}-1}}{(\frac{1+r_1x}{r_2})^{\tfrac{r_1+r_2}{2}}}</math> |
| + | 0<x<\infty</math> where Γ is the gamma function. | ||
*The gamma function is defined by Gamma(t) = integral 0 to infinity x^{t-1} e^{-x} dx. | *The gamma function is defined by Gamma(t) = integral 0 to infinity x^{t-1} e^{-x} dx. | ||
When the value of df1 and df2 are not integers ,then it is converted in to integers. | When the value of df1 and df2 are not integers ,then it is converted in to integers. | ||
| Line 17: | Line 18: | ||
2.x is negative | 2.x is negative | ||
3. df1 or df2<1 ,and df1 ordf2>=10^10 | 3. df1 or df2<1 ,and df1 ordf2>=10^10 | ||
| − | |||
==Examples== | ==Examples== | ||
Revision as of 01:12, 8 January 2014
FDIST(x,df1,df2)
- is the value of the function
- and is degrees of freedom.
Description
- This function gives the value of F probability distribution.
- This distribution is continuous probability distribution and it is called Fisher-Snedecor distribution.
- The F distribution is an asymmetric distribution that has a minimum value of 0, but no maximum value.
- In is the value of the function , is the numerator degrees of freedom and is the denominator degrees of freedom.
- This distribution is the ratio of two chi-square distributions with degrees of freedom r1 and r2, respectively, where each chi-square has first been divided by its degrees of freedom.
- The Probability density function of the F distribution is:
0<x<\infty</math> where Γ is the gamma function.
- The gamma function is defined by Gamma(t) = integral 0 to infinity x^{t-1} e^{-x} dx.
When the value of df1 and df2 are not integers ,then it is converted in to integers.
- This function will give the result as error when
1. any one of the argument is nonnumeric. 2.x is negative 3. df1 or df2<1 ,and df1 ordf2>=10^10
Examples
- FDIST(20.6587,7,3)=0.01526530981
- FDIST(70.120045,12.2,6.35)=0.000011229898
- FDIST(10,1.3,1.5)=0.134947329626
- FDIST(-28,4,6)=NAN
See Also
 is the value of the function
is the value of the function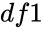 and
and 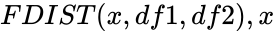 is the value of the function ,
is the value of the function ,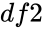 is the denominator degrees of freedom.
is the denominator degrees of freedom.^{\tfrac {r_{1}}{2}}}{\Gamma ({\frac {r_{1}}{2}})\Gamma ({\frac {r_{2}}{2}})}}*{\frac {(x)^{{\tfrac {r_{1}}{2}}-1}}{({\frac {1+r_{1}x}{r_{2}}})^{\tfrac {r_{1}+r_{2}}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/bf128c19052b2d77e9867508e60f25c553dfee41) 0<x<\infty</math> where Γ is the gamma function.
0<x<\infty</math> where Γ is the gamma function.