Difference between revisions of "Manuals/calci/IMSQRT"
Jump to navigation
Jump to search
| Line 38: | Line 38: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] | [http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 08:11, 13 March 2017
IMSQRT(Complexnumber)
- is of the form
Description
- This function gives square root of a complex number.
- IMSQRT(z), where z is the complex number is in the form of "x+iy".
- where x&y are the real numbers. imaginary unit ..
- The square root of a complex number is defined by:
Failed to parse (syntax error): {\displaystyle \sqrt{z}=\sqrt{x+iy}=\sqrt{r.e^{i\theta}}=\sqrt{{r}(cos(\frac{θ}{2})+isin(\frac{θ}{2})}}
- where is the modulus of .
- And is the argument of . Failed to parse (syntax error): {\displaystyle θ=tan^{-1}(y/x)} also Failed to parse (syntax error): {\displaystyle θ∈(-\pi,\pi]} .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
ZOS
- The syntax is to calculate square root of a complex number in ZOS is .
- is of the form
- For e.g.,IMSQRT("9+10i")
- IMSQRT(IMSUB("9+10i","-2-3i"))
Examples
- =IMSQRT("2+3i")=1.67414922803554+0.895977476129838i
- =IMSQRT("-4-5i")=1.09615788950152-2.2806933416653i
- =IMSQRT("7")=2.64575131106459
- =IMSQRT("8i")=2+2i
Related Videos
See Also
References
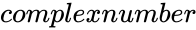 is of the form
is of the form 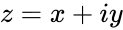
 imaginary unit .
imaginary unit .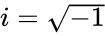 .
.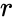 is the modulus of
is the modulus of 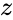 .
. 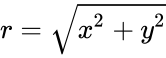
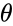 is the argument of
is the argument of 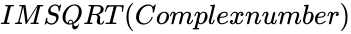 .
.