Difference between revisions of "Manuals/calci/LUCAS"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
==Description== | ==Description== | ||
*This function gives the Lucas series of the numbers. | *This function gives the Lucas series of the numbers. | ||
| − | *Lucas numbers are similar to the Fibonacci | + | *Lucas numbers are similar to the Fibonacci numbers. |
*It is generated by added the last two numbers in the series. | *It is generated by added the last two numbers in the series. | ||
| − | *In <math>LUCAS(n), n </math> is the numbers position, which is used to displaying the numbers in the given range. | + | *In <math>LUCAS(n)</math>, <math>n</math> is the numbers position, which is used to displaying the numbers in the given range. |
*The difference between Lucas and Fibonacci numbers are with the first two terms <math>L_0=2</math> and <math>L_1=1 </math>, but <math>F_0=0</math> and <math>F_1=1</math>. | *The difference between Lucas and Fibonacci numbers are with the first two terms <math>L_0=2</math> and <math>L_1=1 </math>, but <math>F_0=0</math> and <math>F_1=1</math>. | ||
*The Lucas numbers are defined by: <math>L_n=\begin{cases} 2 &if &n=0 \\ | *The Lucas numbers are defined by: <math>L_n=\begin{cases} 2 &if &n=0 \\ | ||
| Line 13: | Line 13: | ||
\end{cases}</math> | \end{cases}</math> | ||
| − | *The sequence of Lucas numbers is 2,1,3,4,7, 11,18,29 | + | *The sequence of Lucas numbers is 2,1,3,4,7,11,18,29.... |
| − | *The relation between Lucas and Fibonacci numbers are: <math> L_n=F_n+2F_{n-1} </math> and <math> F_n=\frac{L_{n-1}+L_{n+1}}{5}</math> | + | *The relation between Lucas and Fibonacci numbers are: |
| − | where L is the Lucas series with <math> L_n</math> is the | + | <math> L_n=F_n+2F_{n-1} </math> |
| − | This function will give the result as error when n is | + | and : |
| + | <math> F_n=\frac{L_{n-1}+L_{n+1}}{5}</math> | ||
| + | where <math>L</math> is the Lucas series with <math> L_n</math> is the <math>n^{th}</math> Lucas number and <math> F_n </math> is the <math>n^{th}</math> Fibonacci number. | ||
| + | This function will, give the result as error when <math>n</math> is non-numeric or n < 0 | ||
==Examples== | ==Examples== | ||
Revision as of 23:52, 3 February 2014
LUCAS(n)
- is the number indicating the position.
Description
- This function gives the Lucas series of the numbers.
- Lucas numbers are similar to the Fibonacci numbers.
- It is generated by added the last two numbers in the series.
- In , is the numbers position, which is used to displaying the numbers in the given range.
- The difference between Lucas and Fibonacci numbers are with the first two terms and , but and .
- The Lucas numbers are defined by:
- The sequence of Lucas numbers is 2,1,3,4,7,11,18,29....
- The relation between Lucas and Fibonacci numbers are:
and : where is the Lucas series with is the Lucas number and is the Fibonacci number.
This function will, give the result as error when is non-numeric or n < 0
Examples
- =LUCAS(5)= 2 1 3 4 7 11
- =LUCAS(0)= 2
- =LUCAS(1)= 2 1
- =LUCAS(3)= 2 1 3 4
- =LUCAS(-1)=Null
 is the number indicating the position.
is the number indicating the position.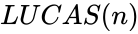 ,
, 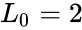 and
and 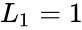 , but
, but 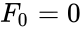 and
and 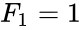 .
.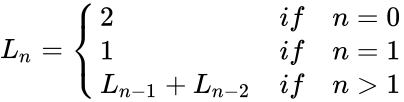
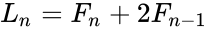 and :
and :
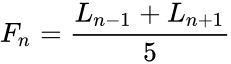 where
where 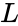 is the Lucas series with
is the Lucas series with 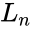 is the
is the 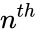 Lucas number and
Lucas number and 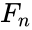 is the
is the