Difference between revisions of "Manuals/calci/MCORREL"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MCORREL (ArrayOfArrays) '''</div><br/> *<math>ArrayOfArrays</math> is set of values. ==Description== *This function is showing the result for m...") |
|||
| (8 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
*It is multiple if there is one variable on one side and a set of variables on the other side. | *It is multiple if there is one variable on one side and a set of variables on the other side. | ||
*If we have a series of <math>n</math> measurements of <math>X</math> and <math>Y</math> written as <math>x_i</math> and <math>y_i</math> where <math>i = 1, 2,...n</math> then the Sample Correlation Coefficient is: | *If we have a series of <math>n</math> measurements of <math>X</math> and <math>Y</math> written as <math>x_i</math> and <math>y_i</math> where <math>i = 1, 2,...n</math> then the Sample Correlation Coefficient is: | ||
| − | + | <math>CORREL(X,Y)= r_{xy}= \frac{\sum_{i=1}^n (x_i-\bar x)(y_i-\bar y)}{\sqrt{ \sum_{i=1}^n (x_i-\bar x)^2 \sum_{i=1}^n (y_i-\bar y)^2}}</math> | |
*<math>\bar x</math> and <math>\bar y</math> are the sample means of <math>X</math> and <math>Y</math>. | *<math>\bar x</math> and <math>\bar y</math> are the sample means of <math>X</math> and <math>Y</math>. | ||
*The above formula is used for simple correlation. | *The above formula is used for simple correlation. | ||
*Now consider the variables x,y and z we define the multiple correlation as: | *Now consider the variables x,y and z we define the multiple correlation as: | ||
| − | <math>R_{zxy}=\sqrt{\frac{r_{xz}^2+r_{yz}^2-2 r_{xz} r_{yz} r_{xy}}{1-r_{xy}^2}</math> | + | <math>R_{zxy}=\sqrt{\frac{r_{xz}^2+r_{yz}^2-2 r_{xz} r_{yz} r_{xy}}{1-r_{xy}^2}}</math> |
*<math>r_{xy}</math> is the correlation of x and y. | *<math>r_{xy}</math> is the correlation of x and y. | ||
*<math>r_{yz}</math> is the correlation of y and z. | *<math>r_{yz}</math> is the correlation of y and z. | ||
| Line 18: | Line 18: | ||
*Here x and y are viewed as the independent variables and z is the dependent variable. | *Here x and y are viewed as the independent variables and z is the dependent variable. | ||
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1.<math>Array of Arrays</math> are non-numeric or different number of data points. | + | 1.<math>Array of Arrays</math> are non-numeric or different number of data points. |
| − | 2.<math>Array of Arrays </math>is empty | + | 2.<math>Array of Arrays </math>is empty |
| − | 3.The denominator value is zero. | + | 3.The denominator value is zero. |
==Examples== | ==Examples== | ||
| + | 1. MCORREL([[10,12,14],[19,43,18],[20,35,90]]) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || -0.035325913054179946 || 0.9496528264568825 | ||
| + | |- | ||
| + | | -0.035325913054179946 || 1 || -0.3466559828504114 | ||
| + | |- | ||
| + | | 0.9496528264568825 || -0.3466559828504114 || 1 | ||
| + | |} | ||
| + | 2. MCORREL([[10,19,18],[-24,90.3,25]]) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 0.8755550584018907 | ||
| + | |- | ||
| + | | 0.8755550584018907 || 1 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=L3Nx7WpozCA|280|center|Multiple Correlation}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 12:58, 25 April 2019
MCORREL (ArrayOfArrays)
- is set of values.
Description
- This function is showing the result for multiple correlation.
- In , are set of values.
- Correlation is a statistical technique which shows the relation of strongly paired variables.When one variable is related to a number of other variables, the correlation is not simple.
- It is multiple if there is one variable on one side and a set of variables on the other side.
- If we have a series of measurements of and written as and where then the Sample Correlation Coefficient is:
- and are the sample means of and .
- The above formula is used for simple correlation.
- Now consider the variables x,y and z we define the multiple correlation as:
- is the correlation of x and y.
- is the correlation of y and z.
- is the correlation of z and x.
- Here x and y are viewed as the independent variables and z is the dependent variable.
- This function will give the result as error when
1. are non-numeric or different number of data points. 2.is empty 3.The denominator value is zero.
Examples
1. MCORREL([[10,12,14],[19,43,18],[20,35,90]])
| 1 | -0.035325913054179946 | 0.9496528264568825 |
| -0.035325913054179946 | 1 | -0.3466559828504114 |
| 0.9496528264568825 | -0.3466559828504114 | 1 |
2. MCORREL([[10,19,18],[-24,90.3,25]])
| 1 | 0.8755550584018907 |
| 0.8755550584018907 | 1 |
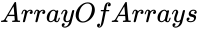 is set of values.
is set of values.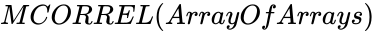 ,
,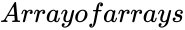 are set of values.
are set of values. measurements of
measurements of 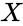 and
and 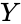 written as
written as 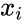 and
and 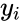 where
where 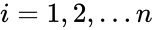 then the Sample Correlation Coefficient is:
then the Sample Correlation Coefficient is: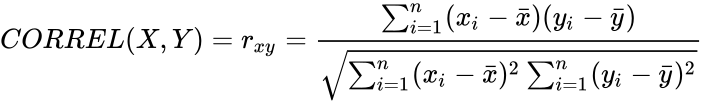
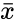 and
and 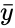 are the sample means of
are the sample means of 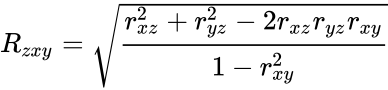
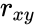 is the correlation of x and y.
is the correlation of x and y. is the correlation of y and z.
is the correlation of y and z. is the correlation of z and x.
is the correlation of z and x.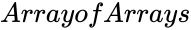 are non-numeric or different number of data points.
2.
are non-numeric or different number of data points.
2.