Difference between revisions of "Manuals/calci/SINC"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*In <math>SINC(X)</math>, <math>X</math> is any real number. | *In <math>SINC(X)</math>, <math>X</math> is any real number. | ||
*The full name of the function is sine cardinal,but it is commonly referred to by its abbreviation, Sinc. | *The full name of the function is sine cardinal,but it is commonly referred to by its abbreviation, Sinc. | ||
| − | *The unnormalized SINC function is defined by | + | *The unnormalized SINC function is defined by : |
| − | |||
| − | |||
| − | |||
| − | |||
<math>SINC(X)=\begin{cases} | <math>SINC(X)=\begin{cases} | ||
1 & for & x=0 \\ | 1 & for & x=0 \\ | ||
| − | + | \frac{Sin x}{x} & Otherwise\\ | |
\end{cases}</math> | \end{cases}</math> | ||
*The normalized SINC function is defined by <math>SINC(X)= \frac{SIN(pi())x}{pi()x}</math> . | *The normalized SINC function is defined by <math>SINC(X)= \frac{SIN(pi())x}{pi()x}</math> . | ||
*The value at x = 0 is defined to be the limiting value Sinc(0) = 1. | *The value at x = 0 is defined to be the limiting value Sinc(0) = 1. | ||
*The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π. | *The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π. | ||
Revision as of 14:35, 9 May 2017
SINC(X)
- is any real number.
Description
- This function shows the value of the cardinal sin function.
- In , is any real number.
- The full name of the function is sine cardinal,but it is commonly referred to by its abbreviation, Sinc.
- The unnormalized SINC function is defined by :
- The normalized SINC function is defined by .
- The value at x = 0 is defined to be the limiting value Sinc(0) = 1.
- The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π.
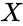 is any real number.
is any real number.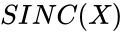 ,
, 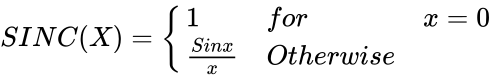
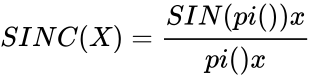 .
.