Difference between revisions of "Manuals/calci/SINC"
Jump to navigation
Jump to search
| (6 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
*The unnormalized SINC function is defined by : | *The unnormalized SINC function is defined by : | ||
<math>SINC(X)=\begin{cases} | <math>SINC(X)=\begin{cases} | ||
| − | 1 & for | + | 1 & for x=0 \\ |
\frac{Sin x}{x} & Otherwise\\ | \frac{Sin x}{x} & Otherwise\\ | ||
\end{cases}</math> | \end{cases}</math> | ||
| − | *The normalized SINC function is defined by <math>SINC(X)= \frac{SIN | + | *The normalized SINC function is defined by <math>SINC(X)= \frac{SIN\pi x}{\pi x}</math> . |
*The value at x = 0 is defined to be the limiting value Sinc(0) = 1. | *The value at x = 0 is defined to be the limiting value Sinc(0) = 1. | ||
*The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π. | *The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π. | ||
| + | |||
| + | ==Examples== | ||
| + | #SINC(9) = 0.04579094280463962 | ||
| + | #SINC(-34) = 0.015561255474118348 | ||
| + | #SINC(-51.7) = 0.019163025320677915 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=9sd4DWragBg|280|center|Cardinal Sin}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/SIN| SIN]] | ||
| + | *[[Manuals/calci/SINH| SINH]] | ||
| + | *[[Manuals/calci/ASINH| ASINH]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Sinc_function SinC] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:33, 31 January 2019
SINC(X)
- is any real number.
Description
- This function shows the value of the cardinal sin function.
- In , is any real number.
- The full name of the function is sine cardinal,but it is commonly referred to by its abbreviation, Sinc.
- The unnormalized SINC function is defined by :
- The normalized SINC function is defined by .
- The value at x = 0 is defined to be the limiting value Sinc(0) = 1.
- The only difference between the two definitions is in the scaling of the independent variable (the x-axis) by a factor of π.
Examples
- SINC(9) = 0.04579094280463962
- SINC(-34) = 0.015561255474118348
- SINC(-51.7) = 0.019163025320677915
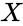 is any real number.
is any real number.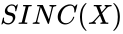 ,
, 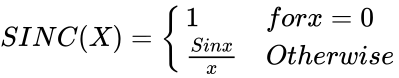
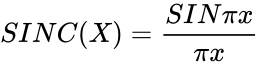 .
.