Manuals/calci/ANTIDIAGONAL
MATRIX (TypeOfMatrix,DimensionsOfMatrix,SeedValuesToUse,IJFunction,PreParameter,IsItInternalCall)
- is the type of the matrix.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle DimensionsOfMatrix } is the order of the Anti diagonal matrix.
Description
- This function gives the matrix satisfying the anti diagonal properties.
- An anti-diagonal matrix is a matrix where all the entries are zero except those on the diagonal going from the lower left corner to the upper right corner (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nearrow} ), known as the anti-diagonal.
- So here we are getting all entries are 0 except from the opposite of main diagonal as 1.
- The properties of anti diagonal matrix are:
- 1.The product of two anti-diagonal matrices is a diagonal matrix.
- 2. If A and D are n×n anti-diagonal and diagonal matrices, respectively, then AD,DA are anti-diagonal.
- 3.All anti-diagonal matrices are also persymmetric.
- To display the different order of matrices then the syntax is MATRIX("anti-diagonal",5).
Examples
- MATRIX("ANTI-DIAGONAL") = 1
- MATRIX("ANTI-DIAGONAL",3)
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
- MATRIX("anti-diagonal",4,200..204)
| 0 | 0 | 0 | 200 |
| 0 | 0 | 201 | 0 |
| 0 | 202 | 0 | 0 |
| 203 | 0 | 0 | 0 |
- MATRIX("anti-diagonal",3,-32.05)
| 0 | 0 | -32.05 |
| 0 | -32.05 | 0 |
| -32.05 | 0 | 0 |
See Also
Related Videos
References
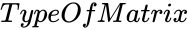 is the type of the matrix.
is the type of the matrix.