Z3
z^3 Language
ZCubes Language (z^3) is an easy to write, natural to read, omni-functional language.
Notable Language Features
z^3 enables high performance computing in Documents, Media and Programs, and works in almost every platform (Windows/Mac/Linux), and in almost every mode (Browsers, Desktops, Servers and Web-Servers, etc.).
z^3 is Highly Scalable, Array-Based, Unit-Sensitive, and comes with all Spreadsheet Functions natively available. This allows powerful programs to be written, to solve simple to highly complex logic, using z^3.
z^3 is routinely used to solve real-world complex enterprise solutions, as well as simple programs. The high expressivity of z^3 Language is further enhanced by natural notations, adopting well established standards in many domains.
This page gives you information about z^3 language, operators, functions etc.
Introduction
Why another programming language? Do we not have enough of them?
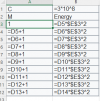
Well, let us try this real world experiment. Go to the best programmer you know. Pick the simplest formula you can think of: E=mc2. Ask how the Energy (E) can be calculated, for a mass (m) of 1kg, 2kg, 3kg,… 10kg and for a constant Speed of Light (3x10^8m/s). And let us just watch the programmer for what happens next. Yes, go ahead and start a stop watch!
Likely that the programmer would pull up a spreadsheet and type formulae notation such as shown below, to do this, within a minute or so.
Or maybe, the programmer would make a program, in a computer language to do this, and will come back to you in about an hour!
Well, this shows the poor state of the current state of the art computer human interaction. Today, an ordinary computer can do billions of operations per second. And even with the best techniques, translating from our human language to computer language takes minutes or hours!
Now, what if,
if we could just say:
Energy:=m*(3*10^8)^2
Energy@1..10
And the results come out:
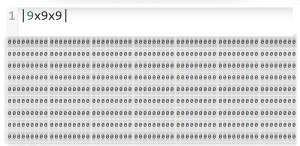
Or let us imagine you wanted to create an array of 9 rows and 9 columns and with 9 cells each in 3 dimensions, and z^3 would give this to you with the command:
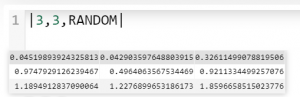
What if you could fill an array of size 3x3 with random numbers and assign it to A using:
Simple! Wow!
That is why we created a simple Language for you and the machine called: z^3. The Powerful, Omni-Functional, ZCubes Language.
Editor and Short cut Keys
Bring down the Symbol Keyboard (⌨) by clicking on the top right of the Code Editor. The ⌨ icon gives access to Operators, Symbols, Units, Greeks, Constants, Code Templates, etc. and more! So feel free to use it anytime!
z^3 Coding Editor is amazing, and more details can be found at coding.zcubes.com.
Typing Code
The Symbol Keyboard is very helpful. Typing on the Code Editor is simple too! There are several helpful ways to express logic and code into the editor.
In the code editor, type the function name (case sensitive), and press Shift+Enter to get parameter expansion. Say CUBEROOT and Shift+Enter will give you CUBEROOT(Number). Or PMT Shift+Enter will give you PMT(Rate,NoPaymentPeriods,PresentValue,FutureValue,Type), to which parameters can be edited and replaced as required.
Generally z^3 Editor automatically shows a listbox with likely functions that you could use given a few letters.
Code expansion also works with things like for, ifelse, switch, zswitch, zif, etc. Simply press Shift+Enter after you type the term.
Say, type FOR and then press Shift+Enter.
Errors are highlighted immediately to give you help with typing things in correctly.
Most functions are Combinatorial. That means you can run them as: PMT((12..20)%,12,1000) or SQRT(1..100) or COMBIN(10..100..10,2..3) etc.
How to type Special Characters
Say you want to type the character for pi. Simply type pi and press Shift+Space. This will automatically convert it to π. To get the between operator, type bet and Shift+Space to get ⧓. 40 deg Shift+Space gives 40°.
Short Cut Keys to Remember
CTRL+G - to convert into Greek Code CTRL+U - Converts SIGMA to Σ Σ - SIGMA - sigma+Ctrl+U SHIFT+ENTER- Gives Parameter Expansion Double tap SHIFT - Toggle Capital and Small Letter [Ex: Convert FRACTAL to fractal and vice verse] CTRL+SPACE - Function Listing
z^3 Commands and Operators
List of Operators
+, -, *, /, ^, % - Arithmetic Operators
| | - Array Function and Creation Operator
.. - Arithmetic and Geometric Series Creation
... - Geometric Series Creation
@ - apply to
# - Series or Special Case Qualifier for Dates, Calci Cells, and Sequences, etc.
<<< - Member or Variable Assignment
<> - Unit Conversion
<+> - Unit Addition
<-> - Unit Substraction
<*> - Unit Multiplication
</> - Unit Division
() - Function Call
[] - Set Creation
- Object Set
- Set Object Membership
. - Member Function Dereferencing.
. mf - Member Function
.$ mf(function, parameters) - Element-wise Function Application
.$$ mf (special – Row-wise Function Application
.$$$ mf (special) – Column-wise Function Application
.$_ mf (special) - Cumulative Function Application (all)
:: - If
::: - switch
⧓ - BETWEEN
⧒ - XLBETWEEN
⧑ - XRBETWEEN
⋈ - XLRBETWEEN
Wrap Operators
.) - To insert a closing left and right parenthesis. .] - To insert a closing left and right square brackets for an array. Example: a.).$_(∑)
Apply Operators
.* - To apply a global function as a member function. SIN is a global function.
Example: a.*SIN() or a.*SUM()
Enhanced Operators
Z Math Operators
➕ ZPLUS ➖ ZSUBTRACT/ZNEGATIVE ➗ ZDIVIDE ✖ ZMULTIPLY ∆ ZPOWER ﹪ ZMOD = ZEQUALS ≠ ZNOTEQUALS ≤ ZLTE ≥ ZGTE > ZGT < ZLT ⎶ ZEQS (Strict Equality) ⍯ ZNES (Strict Not Equality) ⩦ ZFEQ (Floating Value Equality)
Z operators are sensitive to types of parameters, and effortlessly handle Matrices/Arrays, Units, Number Types such as Big Integers, High Precision Decimals, Complex Numbers, Fractions, etc. They parallel the normal operators such as +, -, etc.
Examples:
1.3%%4 ➕2%%3 1..10➕2..30 1m➕34cm a=1..10; b=2; a➗b a=1..10; b=2; a ﹪ b b=(1..9)<>m; b ∆ (1..9)
Hash # Operator
# Operator can have multiple meanings, when used as a binary operator or as suffix. Hash # Operator .
# can be used to (1) arrafy functions, (2) index, search and filter arrays, and (3) index and search Objects. See detailed page Hash # Operator for use cases.
Fabulous ! Operator
! Fabulous ! Operator (Also called Fabulous Operator) ! Operator can have multiple meanings, when used as a suffix. of course, as a prefix, ! represents NOT as in most C like languages.
! can be used to (1) Compute factorial of numbers (including complex numbers etc), (2) Create functions out of strings, (3) Create predicate functions and search functions out of simple notations with regular expressions, strings, etc. See detailed page Fabulous ! Operator for use cases.
Concatenation Operator
Concatenation can be achieved using ⧺ operator, in strings, arrays, etc.
"test" ⧺ "test"
testtest
(1..10)⧺(3..4);
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 3 | 4 |
Join Operator
Joining elements of an array can use the ⚯ operator.
(1..3) ⚯ '-';
1-2-3
More Operators
@: Function Apply Operator
1..100@SIN
~: Transpose Operator
[[[1..10]~]~]~
↑ and ↓: Ascending and Descending Operator
MAGICSQUARE(5)! (1..100)↓ (1..100)↑
Comparison Operators
⧓ - BETWEEN - BET+Ctrl+g, BET+Shift+Space ⧒ - XLBETWEEN - XLBET+Ctrl+g or XLBET+Shift+Space ⧑ - XRBETWEEN - XRBET+Ctrl+g or XRBET+Shift+Space ⋈ - XLRBETWEEN -XLRBET+Ctrl+g or XLRBET+Shift+Space
⧓,⧒,⧒ and ⋈: Between Operators
a=-1; ⧓(1,a,30) a=29; ⧓(1,a,30) //between g a=31; ⧒(1,a,30) //xlbetween g a=30; ⧒(1,a,30) //xlbetween g ⧒(1,2,30) // xlb g ⧒(1,1,30) a=29; ⋈(1,-1..31,30); ⧓(1,-1..5,4); [ ⧓(1,1,30), ⧓(1,0,30), ⧓(1,10,30), ⧓(1,31,30), ⧑(1,29,30), ⧑(1,30,30), ⧑(1,1,30), ⧑(1,30,30), ⋈(1,1,30), ⋈(1,3,30) ]
√: Square Root, Cube Root, Fourth Root and Nth Root Operators
√(3+34) ∛(27.01) √√64 ROOTNTH(1..10,4) // root is first parameter NTHROOT(1..10,4) // root is second parameter NTHROOT(1..100,2) NTHROOT(1..100,4) ROOTNTH(1..100,2) ROOTNTH(1..100,4) 3√81
Logical Statements
If Statements
a=3;
(a<0)::{"whatever"},
{
!(a>4)::
{"whateverelse"},
{"whateverelseleft"}
}
(a>4)::
{"whateverelse"},
{"whateverelseleft"}
Switch Statements
Apart from the conventional Javascript switch statement syntax, z^3 enhances language simplicity with a new style.
The new z^3 switch statements syntax is as follows.
discriminant:::
{
x, y::
/*statements to be executed if x or y is true*/
/*Break is automatically added. */
/*Simply add an empty statement using a simple extra semicolon (;)) */
,
z::
/*statements to be executed if z is true*/
,
default::
}
For example,
b=0;
c=343;
fruits="mango";
fruits:::
{
"apple","tomato"::
b++;
c=3.4;
,
"mango"::
b=34905;
,
default::
b=45.6;
}
[b,c];
switch(a)
{
case b:
case c:
break;
default:
break;
}
If switch discriminant is true, then case clauses can have a condition.
x=1;
y=2;
z=4;
true:::
{
x<2::z=45;
x>2::z=56;
}
z
Loops
a=1;
do
{
a++
}
until(a>20); // do while(!condition)
a; // here this will be 21, since !condition is checked like a do while loop.
a=11;
b=45;
because(a<b)
{
a++
OUTPUT(a)
}
a=11;
do
{
a++
}
unless(a==11);
a;
Function Declarations
function y(x)
{
∵(x<345)
{
∴(x+3434)
}
∵(x>345)
{
∴(x-3434)
}
}
y(13);
The letter Ƒ can also be used instead of the full term function.
Ƒ y(x)
{
∵(x<345)
{
∴(x+3434)
}
∵(x>345)
{
∴(x-3434)
}
}
y(13);
Existential Quantification
a=1..100;
∀a("x<810")
∃a("x<810")
∄a("x<810")
a=1..100;
[∀a("x<810"),∃a("x<810"),∄a("x<810")]
a=1..100;
[∀a("x<810"),∃a("x<810"),(!∄a("x<0"))]
a=1..100;
b= ∀a("y*2<200");
b.result
a=1..100;
b= ∀a("y*2<=50");
a.pick(b.result)
//make a pick operator based on a similar array of true false. or non-existant to get the values out.
//PICK
a=1..100;
b= ∀a("y*2<50");
a.pick(b.result)
z^3 Array Manipulation
Refer z^3 Array Manipulation
Fractions
Refer Fractions
z^3 Units
Refer z^3 Units page
z^3 Constants
| Constants | Value | Abbreviations |
|---|---|---|
| Acceleration Of Gravity- Gee | 9.80665 m·s−2 | %gee |
| Acceleration Of Gravity (Gee, Free-Fall On Earth) | 9.80665 m·s−2 | %g |
| Atomic Mass Constant | 1.66053892173e−27 kg | %atomic |
| Avogadro'S Number | 6.0221412927e23 mol−1 | %avogadro |
| Bohr Magneton | 9.2740096820e−24 J·T−1 | %bohr |
| Bohr Radius | 5.291772109217e−11 m | %bohrradius |
| Boltzmann Constant | 1.380648813e−23 J·K−1 | %boltzmann |
| Characteristic Impedance Of Vacuum | 376.730313461 Ω | %characteristic |
| Classical Electron Radius | 2.817940326727e−15 m | %classical |
| Conductance Quantum | 7.748091734625e−5 S | %conductance |
| Conventional Value Of Josephson Constant | 4.835979e14 Hz·V−1 | %conventional |
| Conventional Value Of Von Klitzing Constant | 25812.807 Ω | |
| Coulomb'S Constant | 8.987551787e9 N·m2·C−2 | |
| Efimov Factor | 22.7 | %efimov |
| Electric Constant Vacuum Permittivity | 8.854187817e−12 F·m−1 | %electric |
| Electron Mass | 9.1093829140e−31 kg | %electronmass |
| Elementary Charge | 1.60217656535e−19 C | %elementary |
| Faraday Constant | 96485.336521C·mol−1 | %faraday |
| Fermi Coupling Constant | 1.1663645e−5 GeV−2 | %fermi |
| Fine-Structure Constant | 7.297352569824e−3 | %fine |
| First Radiation Constant | 3.7417715317e−16 W·m2 | %first |
| First Radiation Constant For Spectral Radiance | 1.19104286953e−16 W·m2·sr−1 | |
| Gas Constant | 8.314462175 J·K−1·mol−1 | %gas |
| Hartree Energy | 4.3597443419e−18 J | %hartree |
| Inverse Conductance Quantum | 12906.403721742 Ω | %inverse |
| Josephson Constant | 4.8359787011e14 Hz·V−1 | %josephson |
| Loschmidt Constant | 2.686780524e25 m−3 | %loschmidt |
| Magnetic Constant Vacuum Permeability | 1.256637061e−6 N·A−2 | |
| Magnetic Flux Quantum | 2.06783375846e−15 Wb | |
| Molar Mass Constant | 1e−3 kg·mol−1 | %molarmass |
| Molar Mass Constant Of Carbon-12 | 1.2e−2 kg·mol−1 | |
| Molar Planck Constant | 3.990312717628e−10 J·s·mol−1 | %molar |
| Molar Volume Of An Ideal Gas At T=273.15K And P=100Kpa | 2.271095321e−2 m3·mol−1 | %molarvolume |
| Molar Volume Of An Ideal Gas At T=273.15K And P=101.325 Kpa | 2.241396820e−2 m3·mol−1 | |
| Newtonian Constant Of Gravitation | 6.6740831e−11 m3·kg−1·s−2 | %newtonian |
| Nuclear Magneton | 5.0507835311e−27 J·T−1 | %nuclear |
| Planck Charge | 1.87554595641e−18 C | %planckcharge |
| Planck Constant | 6.62607004081e−34 J·s | %planck |
| Planck Length | 1.61619997e−35 m | %plancklength |
| Planck Mass | 2.1765113e−8 kg | %planckmass |
| Planck Temperature | 1.41683385e32 K | %plancktemperature |
| Planck Time | 5.3910632e−44 s | %plancktime |
| Proton Mass | 1.67262177774e−27 kg | %proton |
| Quantum Of Circulation | 3.636947552024e−4 m2 s−1 | %quantumof |
| Reduced Planck Constant | 1.05457180013e−34 J·s | |
| Rydberg Constant | 10973731.56853955 m−1 | %rydberg |
| Sackur-Tetrode Constant At T=1 K And P=100Kpa | −1.151707823 | %sackur |
| Sackur-Tetrode Constant At T=1 K And P=101.325 Kpa | −1.164870823 | |
| Second Radiation Constant | 1.438777013e−2 m·K | %second |
| Speed Of Light In Vacuum | 299792458 m·s−1 | %speed |
| Speed Of Sound In Dry Air | 343.2 m·s−1 | |
| Standard Atmosphere | 101325 Pa | %atm |
| Stefan–Boltzmann Constant | 5.67037321e−8 W·m−2·K−4 | %stefan |
| Thomson Cross Section | 6.65245873413e−29 m2 | %thomson |
| Von Klitzing Constant | 25812.807443484 Ω | %von |
| Weak Mixing Angle | 0.222321 | %weak |
| Wien Displacement Law Constant | 2.897772126e−3 m·K | %wien |
ZOS and Calci functions Categorywise
Refer ZOS and Calci functions Categorywise
z^3 API functions
Refer z^3 API Functions page