Difference between revisions of "Manuals/calci/BETADIST"
| Line 5: | Line 5: | ||
==Description== | ==Description== | ||
| − | *This function gives the | + | *This function gives the Cumulative Beta Probability Density function. |
| − | *The beta distribution is a family of | + | *The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by <math>\alpha</math> and <math>\beta</math>. |
| − | *The Beta | + | *The Beta Distribution is also known as the Beta Distribution of the first kind. |
| − | *In BETADIST(x,alpha, | + | *In BETADIST(x,<math>\alpha</math>,<math>\betab</math>,a,b) <math>x</math> is the value between <math>a</math> and <math>b</math>. |
| − | *Normally x | + | *alpha is the value of the shape parameter. |
| − | *The | + | *beta is the value of the shape parameter |
| − | *The formula for the | + | *<math>a</math> and <math>b</math>(optional) are the Lower and Upper limit to the interval of <math>x</math>. |
| − | F(x)=Ix( | + | *Normally <math>x</math> lies between the limit <math>a</math> and <math>b</math>, suppose when we are omitting <math>a</math> and <math>b</math> value, by default <math>x</math> value with in 0 and 1. |
| + | *The Probability Density Function of the beta distribution is: | ||
| + | <math>f(x)=\frac{x^{\alpha-1}(1-x)^{ \beta-1}}{B(\alpha,\beta)},</math> where <math>0 /le x /le 1</math>; <math>/alpha,/beta >0 </math> and <math>B(\alpha,\beta)</math> is the Beta function. | ||
| + | *The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by <math>Ix</math> and is defined as : | ||
| + | <math>F(x)=Ix(\alpha,\beta)=\int_{0}^{x}{t^{α−1}(1−t)^{\beta−1}dt} {B(p,q)}, where <math>0 \le x \le 1</math>0 ; <math>\alpha,\beta>0</math>0 and <math>B(\alpha,\beta)</math> is the Beta function. | ||
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1. Any one of the arguments are non-numeric | + | 1.Any one of the arguments are non-numeric |
| − | 2.alpha or beta< | + | 2.<math>\alpha \le 0</math> or <math>\beta \le 0</math> |
| − | 3.x<a ,x>b, or a=b | + | 3.<math>x<a</math> ,<math>x>b</math>, or <math>a=b</math> |
| − | 4. we are not mentioning the limit values a and b, by default it will consider the standard cumulative beta distribution, a= 0 and b= 1. | + | 4.we are not mentioning the limit values <math>a</math> and <math>b</math>, by default it will consider the standard cumulative beta distribution, <math>a = 0</math> and <math>b = 1</math>. |
==Examples== | ==Examples== | ||
Revision as of 04:06, 3 December 2013
- x is the value between a and b,
- alpha and beta are the value of the shape parameter
- a & b the lower and upper limit to the interval of x.
Description
- This function gives the Cumulative Beta Probability Density function.
- The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} .
- The Beta Distribution is also known as the Beta Distribution of the first kind.
- In BETADIST(x,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \betab} ,a,b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the value between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} .
- alpha is the value of the shape parameter.
- beta is the value of the shape parameter
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and (optional) are the Lower and Upper limit to the interval of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} .
- Normally Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} lies between the limit Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} , suppose when we are omitting Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} value, by default Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} value with in 0 and 1.
- The Probability Density Function of the beta distribution is:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=\frac{x^{\alpha-1}(1-x)^{ \beta-1}}{B(\alpha,\beta)},} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 /le x /le 1} ; Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle /alpha,/beta >0 } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(\alpha,\beta)} is the Beta function.
- The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ix} and is defined as :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x)=Ix(\alpha,\beta)=\int_{0}^{x}{t^{α−1}(1−t)^{\beta−1}dt} {B(p,q)}, where <math>0 \le x \le 1} 0 ; Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha,\beta>0} 0 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(\alpha,\beta)} is the Beta function.
- This function will give the result as error when
1.Any one of the arguments are non-numeric
2.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \le 0}
or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta \le 0}
3.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x<a}
,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x>b}
, or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=b}
4.we are not mentioning the limit values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b}
, by default it will consider the standard cumulative beta distribution, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = 0}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = 1}
.
Examples
- BETADIST(0.4,8,10) = 0.359492343
- BETADIST(3,5,9,2,6) = 0.20603810250
- BETADIST(9,4,2,8,11) = 0.04526748971
- BETADIST(5,-1,-2,4,7) = NAN
See Also
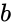 (optional) are the Lower and Upper limit to the interval of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
.
(optional) are the Lower and Upper limit to the interval of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
.