Difference between revisions of "Manuals/calci/BESSELJ"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''BESSELJ(x,n)'''</div><br/> | <div style="font-size:30px">'''BESSELJ(x,n)'''</div><br/> | ||
*<math>x</math> is the value to evaluate the function | *<math>x</math> is the value to evaluate the function | ||
| − | *<math>n</math> is the order of the Bessel function and is an integer | + | *<math>n</math> is the order of the Bessel function and is an integer. |
| + | |||
==Description== | ==Description== | ||
*This function gives the value of the modified Bessel function. | *This function gives the value of the modified Bessel function. | ||
| Line 16: | Line 17: | ||
*This function will give result as error when | *This function will give result as error when | ||
1. <math>x</math> or <math>n</math> is non numeric | 1. <math>x</math> or <math>n</math> is non numeric | ||
| − | 2. <math>n < 0</math>, because <math>n</math> is the order of the function | + | 2. <math>n < 0</math>, because <math>n</math> is the order of the function. |
| + | |||
| + | ==ZOS Section== | ||
| + | *The syntax is to calculate BESSELJ in ZOS is <math>BESSELJ(x,n)</math>. | ||
| + | **<math>x</math> is the value to evaluate the function | ||
| + | **<math>n</math> is the order of the Bessel function and is an integer. | ||
| + | *For e.g.,BESSELJ(0.789..0.901..0.025,5) | ||
| + | |||
==Examples== | ==Examples== | ||
Revision as of 03:25, 11 June 2014
BESSELJ(x,n)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the value to evaluate the function
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} is the order of the Bessel function and is an integer.
Description
- This function gives the value of the modified Bessel function.
- Bessel functions is also called Cylinder Functions because they appear in the solution to Laplace's equation in cylindrical coordinates.
- Bessel's Differential Equation is defined as: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2\frac{d^2 y}{dx^2} + x\frac{dy}{dx} + (x^2 - \alpha^2)y =0}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} is the arbitrary Complex Number.
- But in most of the cases Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} is the non-negative real number.
- The solutions of this equation are called Bessel Functions of order n.
- Bessel functions of the first kind, denoted as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_n(x)}
- The Bessel function of the first kind of order can be expressed as:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_n(x)=\sum_{k=0}^\infty \frac{(-1)^k*(\frac{x}{2})^{n+2k} }{k!\Gamma(n+k+1)}}
- where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma(n+k+1)=(n+k)!} or
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\limits_{0}^{\infty} x^{n+k}*e^{-x} dx} is the Gamma Function.
- This function will give result as error when
1. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
is non numeric
2. , because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
is the order of the function.
ZOS Section
- The syntax is to calculate BESSELJ in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle BESSELJ(x,n)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the value to evaluate the function
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} is the order of the Bessel function and is an integer.
- For e.g.,BESSELJ(0.789..0.901..0.025,5)
Examples
- BESSELJ(2,3) = 0.12894325
- BESSELJ(7,2) = -0.301417224
- BESSELJ(5,1) = -0.327579139
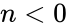 , because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
is the order of the function.
, because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
is the order of the function.