Difference between revisions of "Manuals/calci/LISSAJOUSCURVE"
Jump to navigation
Jump to search
| Line 22: | Line 22: | ||
# LISSAJOUSCURVE("ellipse") | # LISSAJOUSCURVE("ellipse") | ||
[[File:Lissajous_Curve.png]] | [[File:Lissajous_Curve.png]] | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=K_MVFYyVkXQ|280|center|Lissajous}} | ||
| + | |||
==See Also== | ==See Also== | ||
*[[Manuals/calci/FRACTAL | FRACTAL ]] | *[[Manuals/calci/FRACTAL | FRACTAL ]] | ||
*[[Manuals/calci/LISSAJOUS| LISSAJOUS ]] | *[[Manuals/calci/LISSAJOUS| LISSAJOUS ]] | ||
| − | |||
==References== | ==References== | ||
Latest revision as of 14:58, 28 February 2019
LISSAJOUSCURVE (Type,Div,Settings)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Type} is the Type of the curve.
Description
- This function shows the Lissajous curve for each values.
- Lissajous Curve is a parametric plot of the harmonic system.
- It is also called Bowditch Curves.Lissajous used sounds of different frequencies to vibrate a mirror.
- A beam of light reflected from the mirror, was allowed to trace patterns which depended on the frequencies of the sounds – in a setup similar to projectors used in today's laser light shows.
- Lissajous figure is the intersection of two sinusoidal curves, the axes of which are at right angles to each other.
- Mathematically, this translates to a Complex harmonic function:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=A Sin(at+\delta)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=B Sin(bt)}
- The appearance of a figure is highly sensitive to a/b, the ratio of a and b.
- According to the ratio value, the shapes of the figures change in interesting ways.
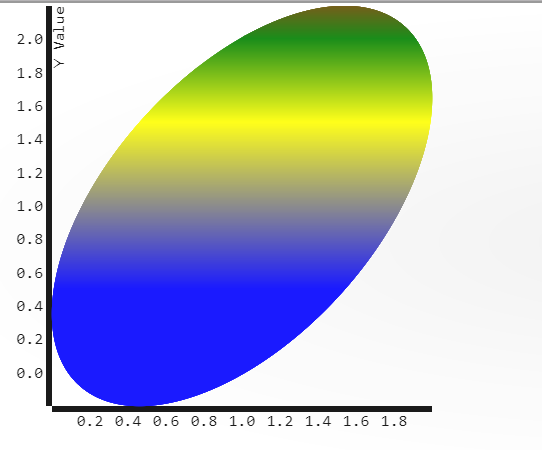
- For a a/b ratio=1, the figure is an ellipse.
- For a=b, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{2}} radians, the figure is a circle.
- For Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} = 0, the figure is a line.
- For a/b = 2, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{4}} , the result is a parabola.
- The Lissajous curve gets more complicated for other ratios, which are closed only if a/b is rational.
Examples
- LISSAJOUSCURVE("ellipse")
Related Videos
See Also
References