Difference between revisions of "Manuals/calci/IM"
| Line 50: | Line 50: | ||
| 0 || 0 || 0 || 0 ||1 | | 0 || 0 || 0 || 0 ||1 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=4lAyqscuTc8|280|center|Types of Matrices}} | ||
| + | |||
==See Also== | ==See Also== | ||
Latest revision as of 13:05, 9 April 2019
- is the order of the matrix.
Description
- This function shows the identity matrix of a given matrix.
- In , is the Order of identity matrix.
- Identity matrix is also called Unit matrix.
- Identity matrix of size n is the nxn square matrix with ones on the main diagonal and zeros on the other entries.
- Identity matrix is denoted by .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_1=[1]} ,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2 =\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_3= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}} ...... Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_n =\begin{bmatrix} 1 & 0 &0 \cdots & 0 \\ 0 & 1 & 0 &\cdots &0 \\ 0 & 0 & 1 &\cdots &0 \\ \vdots & \ddots & \vdots \\ 0 & 0 &0 & \cdots & 1 \end{bmatrix}}
Examples
1.IM(3)
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
2. IM(5)
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 |
Related Videos
See Also
References
 is the order of the matrix.
is the order of the matrix.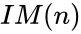 ,
, .
.