Difference between revisions of "Manuals/calci/MATRIXINVERSE"
| (2 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
*This function shows the inverse value of the given matrix. | *This function shows the inverse value of the given matrix. | ||
*In <math>MATRIXINVERSE (a)</math>, <math>a</math> is any square matrix. | *In <math>MATRIXINVERSE (a)</math>, <math>a</math> is any square matrix. | ||
| − | *Inverse of a square matrix is also called reciprocal of a matrix and it is denoted by <math>A^-1</math>. | + | *Inverse of a square matrix is also called reciprocal of a matrix and it is denoted by <math>A^{-1}</math>. |
*Consider the square matrix A has an inverse which should satisfies the following condition <math>|A|\ne 0</math> | *Consider the square matrix A has an inverse which should satisfies the following condition <math>|A|\ne 0</math> | ||
*Also <math>AA^{-1}=I</math>(Identity matrix). | *Also <math>AA^{-1}=I</math>(Identity matrix). | ||
| Line 16: | Line 16: | ||
d & -b \\ | d & -b \\ | ||
-c & a | -c & a | ||
| − | \end{bmatrix}</math> =\frac{1}{ad-bc} \begin{bmatrix} | + | \end{bmatrix}</math> =<math>\frac{1}{ad-bc} \begin{bmatrix} |
d & -b \\ | d & -b \\ | ||
-c & a | -c & a | ||
| Line 35: | Line 35: | ||
\end{bmatrix}}</math> | \end{bmatrix}}</math> | ||
where A=(ei-fh); B=-(di-fg);C=(dh-eg); D=-(bi-ch); E=(ai-cg); F=-(ah-bg); G=(bf-ce) H=-(af-cd);I=(ae-bd) | where A=(ei-fh); B=-(di-fg);C=(dh-eg); D=-(bi-ch); E=(ai-cg); F=-(ah-bg); G=(bf-ce) H=-(af-cd);I=(ae-bd) | ||
| + | |||
| + | ==Examples== | ||
| + | 1. MATRIXINVERSE([4,7;2,6]) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0.6 || -0.7 | ||
| + | |- | ||
| + | | -0.2 || 0.4 | ||
| + | |} | ||
| + | 2. MATRIXINVERSE([1,2,3;0,1,4;5,6,0]) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | -24 || 18 || 5 | ||
| + | |- | ||
| + | | 20 || -15 || -4 | ||
| + | |- | ||
| + | | -5 || 4 || 1 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=Fg7_mv3izR0|280|center|Matrix Inverse}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/MATRIXOPERATORS| MATRIXOPERATORS]] | ||
| + | *[[Manuals/calci/MATRIXDETERMINANT| MATRIXDETERMINANT]] | ||
| + | *[[Manuals/calci/DET| DET]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Invertible_matrix Matrix Inverse] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 13:55, 12 April 2019
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is any matrix.
Description
- This function shows the inverse value of the given matrix.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MATRIXINVERSE (a)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is any square matrix.
- Inverse of a square matrix is also called reciprocal of a matrix and it is denoted by .
- Consider the square matrix A has an inverse which should satisfies the following condition Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |A|\ne 0}
- Also Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AA^{-1}=I} (Identity matrix).
- Consider 2x2 matrix:A=[a b;c d].
- The inverse of matrix A is calculated by
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{-1}={\begin{bmatrix} a & b \\ c & d \end{bmatrix}}^{-1}} =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{det A }\begin{bmatrix} d & -b \\ -c & a \end{bmatrix}} =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}}
- Consider 3x3 matrix A and its inverse is calculated by
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{-1}={\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}}^{-1}} =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{det A }{\begin{bmatrix} A & B & C \\ D & E & F \\ G & H & I \end{bmatrix}}^T } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{det A } {\begin{bmatrix} A & D & G \\ B & E & H \\ C & F & I \end{bmatrix}}}
where A=(ei-fh); B=-(di-fg);C=(dh-eg); D=-(bi-ch); E=(ai-cg); F=-(ah-bg); G=(bf-ce) H=-(af-cd);I=(ae-bd)
Examples
1. MATRIXINVERSE([4,7;2,6])
| 0.6 | -0.7 |
| -0.2 | 0.4 |
2. MATRIXINVERSE([1,2,3;0,1,4;5,6,0])
| -24 | 18 | 5 |
| 20 | -15 | -4 |
| -5 | 4 | 1 |
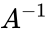 .
.