Difference between revisions of "Manuals/calci/LOGNORMDIST"
Jump to navigation
Jump to search
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''LOGNORMDIST( | + | <div style="font-size:30px">'''LOGNORMDIST(Number,Mean,StandardDeviation,Accuracy)'''</div><br/> |
| − | *<math> | + | *<math>Number</math> is the value. |
| − | * | + | *<math>Mean </math> is the mean value of <math>log(x)</math>, |
| + | *<math>StandardDeviation</math> is the standard deviation value of <math>log(x)</math>. | ||
| + | *<math>Accuracy</math> is correct decimal places for the result. | ||
| + | ** LOGNORMDIST(), returns the cumulative lognormal distribution. | ||
| + | |||
==Description== | ==Description== | ||
| − | |||
*This function gives the value of the cumulative log normal distribution. | *This function gives the value of the cumulative log normal distribution. | ||
*This distribution is the continuous probability distribution. | *This distribution is the continuous probability distribution. | ||
| Line 10: | Line 13: | ||
*Suppose <math>x</math> is Normally Distributed function, then <math> y=ln(x)</math> also Normally Distributed | *Suppose <math>x</math> is Normally Distributed function, then <math> y=ln(x)</math> also Normally Distributed | ||
*<math> z=exp(y)</math> also Normally Distributed. | *<math> z=exp(y)</math> also Normally Distributed. | ||
| − | *Let the Normal Distribution function <math>x</math> and its Mean= <math> | + | *Let the Normal Distribution function <math>x</math> and its Mean= <math>\mu</math>, Standard Deviation = <math>\sigma</math> |
| − | *Then the lognormal cumulative distribution is calculated by:<math>F(x, | + | *Then the lognormal cumulative distribution is calculated by: |
| + | <math>F(x,\mu,\sigma)=\frac{1}{2} \left[1+ erf \left (\frac{ln(x)-\mu)}{\sigma \sqrt{2}}\right)\right ]= \varphi\left[\frac{ln(x)-\mu}{\sigma}\right ]</math> | ||
where <math>erf</math> is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations. | where <math>erf</math> is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations. | ||
*And <math>\phi</math> is the Cumulative Distribution function of the Standard Normal distribution. | *And <math>\phi</math> is the Cumulative Distribution function of the Standard Normal distribution. | ||
*This function will give the result as error when | *This function will give the result as error when | ||
1. Any one of the argument is non-numeric. | 1. Any one of the argument is non-numeric. | ||
| − | 2. Suppose <math> | + | 2. Suppose <math> Number \le 0 </math> or <math> StandardDeviation \le 0</math> |
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate cumulative log normal distribution in ZOS is <math>LOGNORMDIST(Number,Mean,StandardDeviation,Accuracy)</math>. | ||
| + | **<math>Number</math> is the value. | ||
| + | **<math>Mean </math> is the mean value of <math>log(x)</math>. | ||
| + | **<math> StandardDeviation</math> is the standard deviation value of <math>log(x)</math>. | ||
| + | *For e.g.,LOGNORMDIST(10,8.002,4.501) | ||
| + | {{#ev:youtube|rFnzI4pLSuo|280|center|Log Normal Distribution}} | ||
==Examples== | ==Examples== | ||
| − | #LOGNORMDIST(2,5.4,2.76)=0.044061652 | + | #=LOGNORMDIST(2,5.4,2.76) = 0.044061652 |
| − | #LOGNORMDIST(10,24.05,12.95)=0.046543186 | + | #=LOGNORMDIST(10,24.05,12.95) = 0.046543186 |
| − | #LOGNORMDIST(50,87.0036,42.9784)=0.026597569 | + | #=LOGNORMDIST(50,87.0036,42.9784) = 0.026597569 |
| − | #LOGNORMDIST(-10,5,2)= | + | #=LOGNORMDIST(-10,5,2) = #N/A (NUMBER GREATER THAN (OR) NOT EQUAL TO 0) |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|9rMpraPPQ2A|280|center|Lognormal Distribution}} | ||
==See Also== | ==See Also== | ||
| Line 31: | Line 47: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Log-normal_distribution Log-normal distribution] | [http://en.wikipedia.org/wiki/Log-normal_distribution Log-normal distribution] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 09:22, 2 June 2020
LOGNORMDIST(Number,Mean,StandardDeviation,Accuracy)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} is the value.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Mean } is the mean value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle log(x)} ,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle StandardDeviation} is the standard deviation value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle log(x)} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Accuracy}
is correct decimal places for the result.
- LOGNORMDIST(), returns the cumulative lognormal distribution.
Description
- This function gives the value of the cumulative log normal distribution.
- This distribution is the continuous probability distribution.
- Lognomal distribution is also called Galton's distribution.
- A random variable which is log-normally distributed takes only positive real values.
- Suppose Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is Normally Distributed function, then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=ln(x)} also Normally Distributed
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=exp(y)} also Normally Distributed.
- Let the Normal Distribution function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and its Mean= Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , Standard Deviation = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma}
- Then the lognormal cumulative distribution is calculated by:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x,\mu,\sigma)=\frac{1}{2} \left[1+ erf \left (\frac{ln(x)-\mu)}{\sigma \sqrt{2}}\right)\right ]= \varphi\left[\frac{ln(x)-\mu}{\sigma}\right ]} where is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.
- And Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} is the Cumulative Distribution function of the Standard Normal distribution.
- This function will give the result as error when
1. Any one of the argument is non-numeric.
2. Suppose Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number \le 0 }
or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle StandardDeviation \le 0}
ZOS
- The syntax is to calculate cumulative log normal distribution in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LOGNORMDIST(Number,Mean,StandardDeviation,Accuracy)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} is the value.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Mean } is the mean value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle log(x)} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle StandardDeviation} is the standard deviation value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle log(x)} .
- For e.g.,LOGNORMDIST(10,8.002,4.501)
Examples
- =LOGNORMDIST(2,5.4,2.76) = 0.044061652
- =LOGNORMDIST(10,24.05,12.95) = 0.046543186
- =LOGNORMDIST(50,87.0036,42.9784) = 0.026597569
- =LOGNORMDIST(-10,5,2) = #N/A (NUMBER GREATER THAN (OR) NOT EQUAL TO 0)
Related Videos
See Also
References
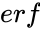 is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.
is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.