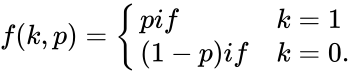Difference between revisions of "Manuals/calci/BERNOULLIDISTRIBUTED"
Jump to navigation
Jump to search
| (2 intermediate revisions by 2 users not shown) | |||
| Line 21: | Line 21: | ||
2. The value of p<0 or p>1. | 2. The value of p<0 or p>1. | ||
| + | ==Examples== | ||
| + | #BERNOULLIDISTRIBUTED(5,0.5) = 0 0 0 0 1 | ||
| + | #BERNOULLIDISTRIBUTED(9,0.8) = 0 1 1 1 1 1 1 1 1 | ||
| + | #BERNOULLIDISTRIBUTED(4,0.87) = 1 1 1 0 | ||
| − | + | ==Related Videos== | |
| − | + | ||
| − | + | {{#ev:youtube|v=O8vB1eInP_8|280|center|Bernoulli Distribution}} | |
| − | + | ||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/BERNOULLI | BERNOULLI]] | ||
| + | *[[Manuals/calci/KURT | KURT]] | ||
| + | *[[Manuals/calci/MULTINOMIAL | MULTINOMIAL]] | ||
| + | |||
| + | ==References== | ||
| + | [http://mathworld.wolfram.com/BernoulliDistribution.html Bernoulli Distribution] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:00, 4 December 2018
BERNOULLIDISTRIBUTED (Numbers,Probability)
- is the number of variables.
- is the value range from 0 to 1.
Description
- This function gives the value of the Bernoulli distribution.
- It is a discrete probability distribution.
- Bernoulli distribution is the theoretical distribution of the number of successes in a finite set of independent trials with a constant probability of success.
- The Bernoulli distribution is simply BINOM(1,P).
- This distribution best describes all situations where a trial is made resulting in either success or failure, such as when tossing a coin, or when modeling the success or failure.
- In , represents the number of variables.
- is the probability value.
- The vaule is ranges from 0 to 1.
- The Bernoulli distribution is defined by: for x={0,1}, where p is the probability that a particular event will occur.
- The probability mass function is :
- This function will give the result as error when
1. Any one of the argument is non numeric. 2. The value of p<0 or p>1.
Examples
- BERNOULLIDISTRIBUTED(5,0.5) = 0 0 0 0 1
- BERNOULLIDISTRIBUTED(9,0.8) = 0 1 1 1 1 1 1 1 1
- BERNOULLIDISTRIBUTED(4,0.87) = 1 1 1 0
Related Videos
See Also
References
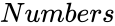 is the number of variables.
is the number of variables.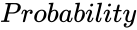 is the value range from 0 to 1.
is the value range from 0 to 1. ,
,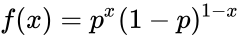 for x={0,1}, where p is the probability that a particular event will occur.
for x={0,1}, where p is the probability that a particular event will occur.