Difference between revisions of "Manuals/calci/IPMT"
| (13 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IPMT( | + | <div style="font-size:30px">'''IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)'''</div><br/> |
| − | *<math> | + | *<math>Rate</math> is the annual rate of interest. |
| − | *<math> | + | *<math>Period</math> is the period of to find the interest rate. |
| − | *<math> | + | *<math>NoPaymentPeriods</math> is the number of installments. |
| − | *<math> | + | *<math>PresentValue</math> is the present value. |
| − | *<math> | + | *<math>FutureValue</math> is the future value. |
| − | *<math> | + | *<math>Type</math> is either 1 or 0. |
| + | **IPMT(), returns the interest payment for an investment for a given period. | ||
| + | |||
==Description== | ==Description== | ||
*This function gives amount of interest for a particular time, according to the periodic, fixed payments and fixed interest rate. | *This function gives amount of interest for a particular time, according to the periodic, fixed payments and fixed interest rate. | ||
*This function can be used to calculate the payments for a loan or the future value of an investment. | *This function can be used to calculate the payments for a loan or the future value of an investment. | ||
| − | *In <math>IPMT( | + | *In <math>IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)</math>, where <math>Rate</math> is the rate of interest for a year |
| − | *<math> | + | *<math>Period</math> is the period for which the interest payment is to be calculated. It must be a value between <math>1</math> and <math>NoPaymentPeriods</math>. |
| − | *<math> | + | *<math>NoPaymentPeriods</math> is the total number of periods over which the loan or investment is to be paid. |
| − | *<math> | + | *<math>PresentValue</math> is the present value of the loan. |
| − | *<math> | + | *<math>FutureValue</math> is the future value of the loan, at the end of <math>NoPaymentPeriods</math> payment. |
| − | *<math> | + | *<math>Type</math> is the number <math>0</math> or <math>1</math>. |
*When type value is <math>0</math> means the payment is made at the end of the period and type value is <math>1</math> means the payment is made at the beginning of the period | *When type value is <math>0</math> means the payment is made at the end of the period and type value is <math>1</math> means the payment is made at the beginning of the period | ||
| − | *Here the arguments <math> | + | *Here the arguments <math>FutureValue</math> and <math>Type</math> are optional. |
| − | *Suppose we omit the value of <math> | + | *Suppose we omit the value of <math>FutureValue</math>, then it will consider the value as <math>0</math>. |
| − | *Also when we are not giving the <math> | + | *Also when we are not giving the <math>Type</math> value, the default value is <math>0</math>. |
| − | *Suppose we calculate the monthly payments instead of annual payment, for the argument <math> | + | *Suppose we calculate the monthly payments instead of annual payment, for the argument <math>Rate</math> we have to divide by <math>12</math> and the <math>np</math> value we have multiply with <math>12</math>. |
| − | *For e.g. The monthly payments on a 5 year loan at 10% annual interest, we have to give the arguments <math> | + | *For e.g. The monthly payments on a 5 year loan at 10% annual interest, we have to give the arguments <math>Rate</math> and <math>NoPaymentPeriods</math> as 10%/12 for <math>Rate</math> and 5*12 for <math>NoPaymentPeriods</math>. |
*This function will give result as error when | *This function will give result as error when | ||
Any one of the argument is non-numeric | Any one of the argument is non-numeric | ||
| − | <math> | + | <math>Period < 0</math> or <math>period > NoPaymentPeriods</math> |
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate amount of interest for a particular time in ZOS is | ||
| + | <math>IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)</math> | ||
| + | **<math>Rate</math> is the annual rate of interest. | ||
| + | **<math>Periods</math> is the period of to find the interest rate. | ||
| + | **<math>NoPaymentPeriods</math> is the number of installments. | ||
| + | **<math>PresentValue</math> is the present value. | ||
| + | **<math>FutureValue</math> is the future value. | ||
| + | **<math>Type</math> is either 1 or 0. | ||
| + | *For e.g., | ||
==Examples== | ==Examples== | ||
| − | *Calculate the interest payment during half yearly 1 and 2 of a loan for 50,000, that is to be reduced to 10,000 over a period of 3 years, by a series of constant half-yearly payments. | + | *1.Calculate the interest payment during half yearly 1 and 2 of a loan for 50,000, that is to be reduced to 10,000 over a period of 3 years, by a series of constant half-yearly payments. |
*Interest is charged at a rate of 4.5% per year and the payment is made at the beginning of each half year. | *Interest is charged at a rate of 4.5% per year and the payment is made at the beginning of each half year. | ||
| − | *IPMT(4.5%/2,3,2*2,50000,10000,1)=-454. | + | *IPMT(4.5%/2,3,2*2,50000,10000,1)= -454.78404196736113 |
| − | 2.The interest payment for a $55000 investment that earns 7.50% annually for 15 years. | + | *2.The interest payment for a $55000 investment that earns 7.50% annually for 15 years. |
*The interest payment is calculated for the 5th year and payments are due at the end of each year. | *The interest payment is calculated for the 5th year and payments are due at the end of each year. | ||
IPMT(7.5%/1, 5, 15*1, 55000)=-3418.570 | IPMT(7.5%/1, 5, 15*1, 55000)=-3418.570 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|QMvsIFXU3z4|280|center|IPMT}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/PMT| PMT]] | ||
| + | *[[Manuals/calci/PPMT| PPMT]] | ||
| + | *[[Manuals/calci/PV| PV]] | ||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/ | + | [http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] |
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 17:34, 29 June 2018
IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)
- is the annual rate of interest.
- is the period of to find the interest rate.
- is the number of installments.
- is the present value.
- is the future value.
- is either 1 or 0.
- IPMT(), returns the interest payment for an investment for a given period.
Description
- This function gives amount of interest for a particular time, according to the periodic, fixed payments and fixed interest rate.
- This function can be used to calculate the payments for a loan or the future value of an investment.
- In , where is the rate of interest for a year
- is the period for which the interest payment is to be calculated. It must be a value between and .
- is the total number of periods over which the loan or investment is to be paid.
- is the present value of the loan.
- is the future value of the loan, at the end of payment.
- is the number or .
- When type value is means the payment is made at the end of the period and type value is means the payment is made at the beginning of the period
- Here the arguments and are optional.
- Suppose we omit the value of , then it will consider the value as .
- Also when we are not giving the value, the default value is .
- Suppose we calculate the monthly payments instead of annual payment, for the argument we have to divide by and the value we have multiply with .
- For e.g. The monthly payments on a 5 year loan at 10% annual interest, we have to give the arguments and as 10%/12 for and 5*12 for .
- This function will give result as error when
Any one of the argument is non-numeric or
ZOS
- The syntax is to calculate amount of interest for a particular time in ZOS is
- is the annual rate of interest.
- is the period of to find the interest rate.
- is the number of installments.
- is the present value.
- is the future value.
- is either 1 or 0.
- For e.g.,
Examples
- 1.Calculate the interest payment during half yearly 1 and 2 of a loan for 50,000, that is to be reduced to 10,000 over a period of 3 years, by a series of constant half-yearly payments.
- Interest is charged at a rate of 4.5% per year and the payment is made at the beginning of each half year.
- IPMT(4.5%/2,3,2*2,50000,10000,1)= -454.78404196736113
- 2.The interest payment for a $55000 investment that earns 7.50% annually for 15 years.
- The interest payment is calculated for the 5th year and payments are due at the end of each year.
IPMT(7.5%/1, 5, 15*1, 55000)=-3418.570
Related Videos
See Also
References
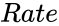 is the annual rate of interest.
is the annual rate of interest.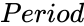 is the period of to find the interest rate.
is the period of to find the interest rate. is the number of installments.
is the number of installments.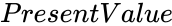 is the present value.
is the present value.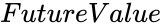 is the future value.
is the future value.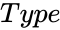 is either 1 or 0.
is either 1 or 0.