Difference between revisions of "Manuals/calci/LN"
Jump to navigation
Jump to search
| (10 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''LN( | + | <div style="font-size:30px">'''LN(Number)'''</div><br/> |
| − | *where <math> | + | *where <math>Number</math> is the any positive real number. |
| + | **LN() returns the natural logarithm of a number. | ||
==Description== | ==Description== | ||
| Line 6: | Line 7: | ||
*<math>LN</math> is the logarithm in which the base is the irrational number <math>e</math> (<math>e</math>= 2.71828...). | *<math>LN</math> is the logarithm in which the base is the irrational number <math>e</math> (<math>e</math>= 2.71828...). | ||
*For example, <math>ln_10 = loge_10 \approx 2.30258</math> | *For example, <math>ln_10 = loge_10 \approx 2.30258</math> | ||
| − | * | + | *It was formely also called Hyperbolic logarithm. |
| + | *And also called Napierian logarithm. | ||
*The constant <math>e</math> is called Euler's number. | *The constant <math>e</math> is called Euler's number. | ||
*The Natural Logarithm is denoted by <math>ln(x)</math> or <math>log e(x)</math>. | *The Natural Logarithm is denoted by <math>ln(x)</math> or <math>log e(x)</math>. | ||
*where <math>x</math> is the Positive real number. | *where <math>x</math> is the Positive real number. | ||
| − | *The ln(x) is the inverse function of the exponential function e^ln(x)=x if x>0. | + | *The <math>ln(x)</math> is the inverse function of the exponential function <math>e^{ln(x)}=x</math> if <math>x>0</math>. |
| − | ln(e^x)=x | + | *<math>ln(e^x)=x</math> |
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate Natural logarithm in ZOS is <math>LN(number)</math>. | ||
| + | **where <math>number</math> is the any positive real number. | ||
| + | *For e.g.,LN(20..23) | ||
| + | {{#ev:youtube|OCirVf3pulA|280|center|Natural Logarithm}} | ||
==Examples== | ==Examples== | ||
| Line 17: | Line 25: | ||
*=LN(8.3) = 2.116255515 | *=LN(8.3) = 2.116255515 | ||
*=LN(1) = 0 | *=LN(1) = 0 | ||
| − | *=LN(0) = INFINITY | + | *=LN(0) = -INFINITY |
*=LN(-20) = NAN | *=LN(-20) = NAN | ||
*=LN(exp(5)) = 5 | *=LN(exp(5)) = 5 | ||
*=EXP(LN(7)) = 7 | *=EXP(LN(7)) = 7 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|eavkIcjXchI|280|center|Natural Logarithm}} | ||
==See Also== | ==See Also== | ||
*[[Manuals/calci/LOG | LOG]] | *[[Manuals/calci/LOG | LOG]] | ||
*[[Manuals/calci/EXP | EXP]] | *[[Manuals/calci/EXP | EXP]] | ||
| − | |||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Natural_logarithm Natural Logarithm] | [http://en.wikipedia.org/wiki/Natural_logarithm Natural Logarithm] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 04:52, 8 June 2020
LN(Number)
- where is the any positive real number.
- LN() returns the natural logarithm of a number.
Description
- This function gives the Natural Logarithm of a number.
- is the logarithm in which the base is the irrational number (= 2.71828...).
- For example,
- It was formely also called Hyperbolic logarithm.
- And also called Napierian logarithm.
- The constant is called Euler's number.
- The Natural Logarithm is denoted by or .
- where is the Positive real number.
- The is the inverse function of the exponential function if .
ZOS
- The syntax is to calculate Natural logarithm in ZOS is .
- where is the any positive real number.
- For e.g.,LN(20..23)
Examples
- =LN(15) = 2.708050201
- =LN(8.3) = 2.116255515
- =LN(1) = 0
- =LN(0) = -INFINITY
- =LN(-20) = NAN
- =LN(exp(5)) = 5
- =EXP(LN(7)) = 7
Related Videos
See Also
References
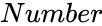 is the any positive real number.
is the any positive real number.
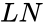 is the logarithm in which the base is the irrational number
is the logarithm in which the base is the irrational number 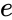 (
(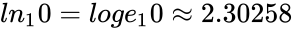
 or
or 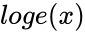 .
. is the Positive real number.
is the Positive real number.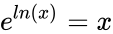 if
if 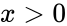 .
.
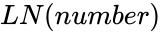 .
.
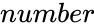 is the any positive real number.
is the any positive real number.