Difference between revisions of "Manuals/calci/PI"
Jump to navigation
Jump to search
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''PI()'''</div><br/> | <div style="font-size:30px">'''PI()'''</div><br/> | ||
| − | |||
==Description== | ==Description== | ||
*This function gives the value of <math>pi</math>. | *This function gives the value of <math>pi</math>. | ||
| − | *The <math>pi</math> | + | *The <math>pi</math> is a mathematical constant with a value approximate to 3.14159. |
*It is denoted by the Greek letter <math>\Pi</math>. | *It is denoted by the Greek letter <math>\Pi</math>. | ||
*<math>\Pi</math> is commonly defined as the ratio of a circle's circumference <math>C</math> to its diameter <math>d</math>. | *<math>\Pi</math> is commonly defined as the ratio of a circle's circumference <math>C</math> to its diameter <math>d</math>. | ||
| − | *So <math>\Pi =\frac {C}{d}</math>, the ratio <math> \frac {C}{d}</math> | + | *So <math>\Pi =\frac {C}{d}</math>, the ratio <math> \frac {C}{d}</math> is constant, and it is not considering the circle's size. |
| − | *<math>\Pi</math> | + | *<math>\Pi</math> is a transcendental number and irrational number. |
| − | *Being an irrational number,<math>\Pi</math> cannot be expressed exactly as a ratio of any two integers . | + | *Being an irrational number, <math>\Pi</math> cannot be expressed exactly as a ratio of any two integers . |
*But we can express as the fraction <math>\frac {22}{7}</math> is approximate to the <math>\Pi</math> value , also no fraction can be its exact value. | *But we can express as the fraction <math>\frac {22}{7}</math> is approximate to the <math>\Pi</math> value , also no fraction can be its exact value. | ||
==Examples== | ==Examples== | ||
| − | #= | + | #=PI() = 3.141592653589793 |
| − | #= | + | #=PI()/4 = 0.785398163 |
| − | #= | + | #=PI()/180 = 0.017453293 |
| − | #= | + | #=PI()/(22/7) = 0.999597663 |
| − | #= | + | #=PI()*(5^2) = 78.53981634(Area of circle with r=5) |
| − | #=2* | + | #=2*PI()*5 = 31.41592654(Circumference of a circle with r=5). |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|jyLRpr2P0MQ|280|center|PI}} | ||
==See Also== | ==See Also== | ||
| − | *[[Manuals/calci/SIN | SIN | + | *[[Manuals/calci/SIN | SIN ]] |
*[[Manuals/calci/COS | COS ]] | *[[Manuals/calci/COS | COS ]] | ||
| − | *[[Manuals/calci/TAN |TAN | + | *[[Manuals/calci/TAN | TAN ]] |
==References== | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Pi Pi] | ||
Latest revision as of 09:26, 10 October 2015
PI()
Description
- This function gives the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle pi} .
- The Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle pi} is a mathematical constant with a value approximate to 3.14159.
- It is denoted by the Greek letter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi} is commonly defined as the ratio of a circle's circumference to its diameter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} .
- So Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi =\frac {C}{d}} , the ratio Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {C}{d}} is constant, and it is not considering the circle's size.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi} is a transcendental number and irrational number.
- Being an irrational number, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi} cannot be expressed exactly as a ratio of any two integers .
- But we can express as the fraction Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {22}{7}} is approximate to the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi} value , also no fraction can be its exact value.
Examples
- =PI() = 3.141592653589793
- =PI()/4 = 0.785398163
- =PI()/180 = 0.017453293
- =PI()/(22/7) = 0.999597663
- =PI()*(5^2) = 78.53981634(Area of circle with r=5)
- =2*PI()*5 = 31.41592654(Circumference of a circle with r=5).
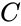 to its diameter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d}
.
to its diameter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d}
.