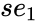Difference between revisions of "Manuals/calci/LOGEST"
Jump to navigation
Jump to search
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | =LOGEST( | + | <div style="font-size:30px">'''LOGEST (YRange,XRange,Constant,Stats)'''</div><br/> |
where, | where, | ||
| − | *<math> | + | *<math>YRange</math> is a set of Y values, |
| − | *<math> | + | *<math>XRange</math> is an optional set of X values, |
| − | *<math> | + | *<math>Constant</math> is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 1, |
| − | *<math> | + | *<math>Stats</math> is a logical value TRUE or FALSE, that decides whether to return additional regression statistics. |
| − | + | **LOGEST() is an array function that calculates the exponential curve that fits the data values and returns an array of values that describes the curve. | |
| − | LOGEST() is an array function that calculates the exponential curve that fits the data values and returns an array of values that describes the curve. | ||
== Description == | == Description == | ||
| − | *If ' | + | *If 'YRange' is the set of dependent variable, 'XRange' is the set of independent variable, 'm' is a constant base for X value and 'b' is constant (Y-intercept), |
then equation for curve is - | then equation for curve is - | ||
| Line 18: | Line 17: | ||
*For multiple ranges of X-values, | *For multiple ranges of X-values, | ||
| − | <math>Y = (b*(m1^X1)*(m2^X2)*......)</math> | + | <math>Y = (b*(m1^{X1})*(m2^{X2})*......)</math> |
| − | *Argument values <math> | + | *Argument values <math>XRange</math> and <math>YRange</math> should be numeric, else Calci displays NaN error message. |
| − | *The length of array of | + | *The length of array of XRange values should be equal to length of array of YRange values, else Calci displays #NULL error message. |
| − | *<math> | + | *<math>Constant</math> is a logical value that decides whether to make constant 'b' equal to 1. |
| − | *If <math> | + | *If <math>Constant</math> = TRUE or omitted, 'b' is calculated normally. If <math>Constant</math> = FALSE, 'b' is made equal to 1. |
| − | *<math> | + | *<math>Stats</math> is a logical value that decides whether to display additional regression statistics. |
| − | *If <math> | + | *If <math>Stats</math> = TRUE, calci returns additional regresstion statistics. If <math>Stats</math> = FALSE or omitted, Calci returns the values of 'm coefficients' and the constant 'b'. |
| − | *When there is only one independent X variable, | + | *When there is only one independent X variable, Y intercept (b) can be calculated using following formulas - |
<math>Y intercept (b) = INDEX(LOGEST(Y, X),2) </math> | <math>Y intercept (b) = INDEX(LOGEST(Y, X),2) </math> | ||
| − | *The additional regression | + | *The additional regression is displayed in the following format where each statistic value is described as below- |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | | <math>m_n</math> || <math>m_ | + | | <math>m_n</math> || <math>m_{n-1}</math> || --- || <math>m_1</math> || <math>b</math> |
|- | |- | ||
| − | | <math>se_n</math> || <math>se_ | + | | <math>se_n</math> || <math>se_{n-1}</math> || --- || <math>se_1</math> || <math>se_b</math> |
|- | |- | ||
| <math>r_2</math> || <math>se_y</math> || || || | | <math>r_2</math> || <math>se_y</math> || || || | ||
| Line 40: | Line 39: | ||
| <math>F</math> || <math>d_f</math> || || || | | <math>F</math> || <math>d_f</math> || || || | ||
|- | |- | ||
| − | | <math>ss_ | + | | <math>ss_{reg}</math> || <math>ss_{resld}</math> || || || |
|} | |} | ||
| − | + | *<math>m_n</math> is an array of constant base values for curve equation | |
| − | <math>m_n</math> is an array of constant base values for curve equation | + | *<math>b</math> is the constant value of Y when X=0 |
| − | <math>b</math> is the constant value of Y when X=0 | + | *<math>se_1</math> is the standard error value for m1 |
| − | <math>se_1</math> is the standard error value for m1 | + | *<math>se_b</math> is the standard error value for constant b |
| − | <math>se_b</math> is the standard error value for constant b | + | *<math>r_2</math> is the coefficient of determination |
| − | <math>r_2</math> is the coefficient of determination | + | *<math>se_y</math> is the standard error value for Y estimate |
| − | <math>se_y</math> is the standard error value for Y estimate | + | *<math>F</math> is the observed F value |
| − | <math>F</math> is the observed F value | + | *<math>d_f</math> is the number of degrees of freedom |
| − | <math>d_f</math> is the number of degrees of freedom | + | *<math>ss_{reg}</math> is the regression sum of squares |
| − | <math>ss_ | + | *<math>ss_{resld}</math> is the residual sum of squares |
| − | <math>ss_ | ||
== Examples == | == Examples == | ||
| Line 97: | Line 95: | ||
|} | |} | ||
| − | Example | + | '''Example 1''': With single range of X values - |
| − | =LOGEST(C2:C6,A2:A6,TRUE,TRUE) : Displays all the regression statistics for curve with Y values in | + | =LOGEST(C2:C6,A2:A6,TRUE,TRUE) : Displays all the regression statistics for curve <br />with Y values in cells C2 to C6 and X values in cells A2 to A6. |
<div id="5SpaceContent" class="zcontent" align="left"> | <div id="5SpaceContent" class="zcontent" align="left"> | ||
| Line 122: | Line 120: | ||
|} | |} | ||
| − | |||
| − | =LOGEST(C2:C6,A2:B6,TRUE,TRUE) : Displays all the regression statistics for curve with Y values in | + | '''Example 2''': With multiple range of X values - |
| + | |||
| + | =LOGEST(C2:C6,A2:B6,TRUE,TRUE) : Displays all the regression statistics for curve <br />with Y values in cells C2 to C6 and X values in cells A2 to B6. | ||
<div id="5SpaceContent" class="zcontent" align="left"> | <div id="5SpaceContent" class="zcontent" align="left"> | ||
| Line 145: | Line 144: | ||
|} | |} | ||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|fp5yFpzAJ7g|280|center|LOGEST}} | ||
| + | |||
== See Also == | == See Also == | ||
| − | *[[Manuals/calci/ | + | *[[Manuals/calci/LINEST| LINEST]] |
== References == | == References == | ||
| Line 153: | Line 156: | ||
*[http://en.wikipedia.org/wiki/Curve_fitting Curve Fitting] | *[http://en.wikipedia.org/wiki/Curve_fitting Curve Fitting] | ||
*[http://en.wikipedia.org/wiki/Linear_equation Linear Equation] | *[http://en.wikipedia.org/wiki/Linear_equation Linear Equation] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:19, 22 August 2018
LOGEST (YRange,XRange,Constant,Stats)
where,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle YRange} is a set of Y values,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle XRange} is an optional set of X values,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Constant} is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 1,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Stats}
is a logical value TRUE or FALSE, that decides whether to return additional regression statistics.
- LOGEST() is an array function that calculates the exponential curve that fits the data values and returns an array of values that describes the curve.
Description
- If 'YRange' is the set of dependent variable, 'XRange' is the set of independent variable, 'm' is a constant base for X value and 'b' is constant (Y-intercept),
then equation for curve is -
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y= b*m^X}
- For multiple ranges of X-values,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y = (b*(m1^{X1})*(m2^{X2})*......)}
- Argument values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle XRange} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle YRange} should be numeric, else Calci displays NaN error message.
- The length of array of XRange values should be equal to length of array of YRange values, else Calci displays #NULL error message.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Constant} is a logical value that decides whether to make constant 'b' equal to 1.
- If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Constant} = TRUE or omitted, 'b' is calculated normally. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Constant} = FALSE, 'b' is made equal to 1.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Stats} is a logical value that decides whether to display additional regression statistics.
- If = TRUE, calci returns additional regresstion statistics. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Stats} = FALSE or omitted, Calci returns the values of 'm coefficients' and the constant 'b'.
- When there is only one independent X variable, Y intercept (b) can be calculated using following formulas -
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y intercept (b) = INDEX(LOGEST(Y, X),2) }
- The additional regression is displayed in the following format where each statistic value is described as below-
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_n} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{n-1}} | --- | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle se_n} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle se_{n-1}} | --- | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle se_b} | |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_2} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle se_y} | |||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_f} | |||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ss_{reg}} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ss_{resld}} |
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_n} is an array of constant base values for curve equation
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} is the constant value of Y when X=0
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle se_1} is the standard error value for m1
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle se_b} is the standard error value for constant b
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_2} is the coefficient of determination
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle se_y} is the standard error value for Y estimate
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} is the observed F value
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_f} is the number of degrees of freedom
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ss_{reg}} is the regression sum of squares
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ss_{resld}} is the residual sum of squares
Examples
| X1 values | X2 values | Y values | |
| 1 | 15 | 5 | |
| 2 | 17 | 9 | |
| 3 | 23 | 11 | |
| 4 | 28 | 16 | |
| 5 | 30 | 20 |
Example 1: With single range of X values -
=LOGEST(C2:C6,A2:A6,TRUE,TRUE) : Displays all the regression statistics for curve
with Y values in cells C2 to C6 and X values in cells A2 to A6.
| 1.3976542375431584 | 4.015612511401349 |
| 0.035964826100314505 | 0.11928183382512401 |
| 0.9665390759484563 | 0.11373076612886521 |
| 86.65681866342828 | 3 |
| 1.1208788400613339 | 0.038804061492775904 |
Example 2: With multiple range of X values -
=LOGEST(C2:C6,A2:B6,TRUE,TRUE) : Displays all the regression statistics for curve
with Y values in cells C2 to C6 and X values in cells A2 to B6.
| 0.9684996526566505 | 1.593646236498643 |
| 0.05737674420683413 | 0.23878654115432985 |
| 0.9710443899207976 | 0.12957493182116453 |
| 33.53562184546261 | 2 |
| 1.1261035756411908 | 0.03357932591291887 |
Related Videos
See Also
References
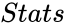 = TRUE, calci returns additional regresstion statistics. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Stats}
= FALSE or omitted, Calci returns the values of 'm coefficients' and the constant 'b'.
= TRUE, calci returns additional regresstion statistics. If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Stats}
= FALSE or omitted, Calci returns the values of 'm coefficients' and the constant 'b'.