Difference between revisions of "Manuals/calci/HILBERT"
Jump to navigation
Jump to search
| (3 intermediate revisions by 2 users not shown) | |||
| Line 17: | Line 17: | ||
*Here MATRIX("hilbert") gives the hilbert matrices with a decimal places . | *Here MATRIX("hilbert") gives the hilbert matrices with a decimal places . | ||
*i.e., For 1/2 it will show 0.5, 1/3 will show 0.333 and so on. | *i.e., For 1/2 it will show 0.5, 1/3 will show 0.333 and so on. | ||
| + | |||
| + | ==Examples== | ||
| + | *1.MATRIX("hilbert")= 1 | ||
| + | *2.MATRIX("hilbert",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 0.5 || 0.3333333333333333 | ||
| + | |- | ||
| + | | 0.5 || 0.3333333333333333 || 0.25 | ||
| + | |- | ||
| + | | 0.3333333333333333|| 0.25 || 0.2 | ||
| + | |} | ||
| + | *3.MATRIX("hilbert",5) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 0.5 || 0.3333333333333333 || 0.25 ||0.2 | ||
| + | |- | ||
| + | | 0.5 || 0.3333333333333333 || 0.25 || 0.2 || 0.16666666666666666 | ||
| + | |- | ||
| + | | 0.3333333333333333|| 0.25 || 0.2 || 0.16666666666666666 || 0.14285714285714285 | ||
| + | |- | ||
| + | | 0.25 || 0.2 || 0.16666666666666666 || 0.14285714285714285 || 0.125 | ||
| + | |- | ||
| + | |0.2 || 0.16666666666666666 || 0.14285714285714285 || 0.125 || 0.1111111111111111 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|B-WCRleUyTk|280|center|Hilbert Matrix}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/HADAMARD| HADAMARD]] | ||
| + | *[[Manuals/calci/HESSENBERG| HESSENBERG]] | ||
| + | *[[Manuals/calci/CIRCULANT| CIRCULANT]] | ||
| + | *[[Manuals/calci/HANKEL| HANKEL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Hilbert_matrix Hilbert matrix] | ||
Latest revision as of 01:12, 26 October 2015
MATRIX("HILBERT",order)
- is the order of the Hilbert matrix.
Description
- This function gives matrix of order 3x3 with the property of Hilbert.
- A Hilbert matrix, is a square matrix with entries being the unit fractions. i.e.,.
- The Hilbert matrix is an example of a Hankel matrix.
- The Hilbert matrix is symmetric and positive definite.
- Also Hilbert matrices are canonical examples of ill-conditioned matrices, making them notoriously difficult to use in numerical computation.
- Here MATRIX("hilbert") gives the hilbert matrices with a decimal places .
- i.e., For 1/2 it will show 0.5, 1/3 will show 0.333 and so on.
Examples
- 1.MATRIX("hilbert")= 1
- 2.MATRIX("hilbert",3)
| 1 | 0.5 | 0.3333333333333333 |
| 0.5 | 0.3333333333333333 | 0.25 |
| 0.3333333333333333 | 0.25 | 0.2 |
- 3.MATRIX("hilbert",5)
| 1 | 0.5 | 0.3333333333333333 | 0.25 | 0.2 |
| 0.5 | 0.3333333333333333 | 0.25 | 0.2 | 0.16666666666666666 |
| 0.3333333333333333 | 0.25 | 0.2 | 0.16666666666666666 | 0.14285714285714285 |
| 0.25 | 0.2 | 0.16666666666666666 | 0.14285714285714285 | 0.125 |
| 0.2 | 0.16666666666666666 | 0.14285714285714285 | 0.125 | 0.1111111111111111 |
 is the order of the Hilbert matrix.
is the order of the Hilbert matrix.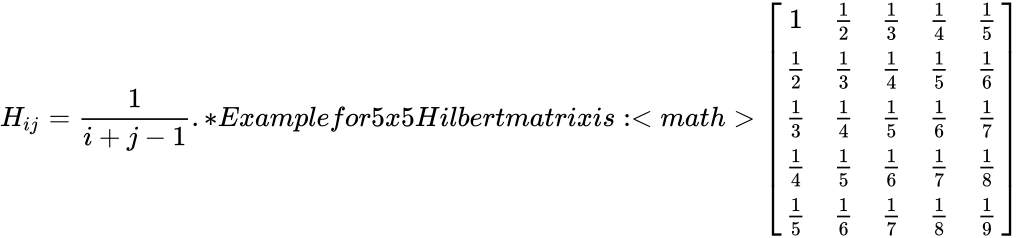 .
.