Manuals/calci/HANKEL
Jump to navigation
Jump to search
MATRIX (TypeOfMatrix,DimensionsOfMatrix,SeedValuesToUse,IJFunction,PreParameter,IsItInternalCall)
- is the type of the matrix.
- is the order of the Hankel matrix.
Description
- This function gives the matrix with the property of hankel matrix.
- A hankel matrix is a square matrix with constant skew diagonals.
- If the i,j element of Hankel matrix A is denoted , then we have
.
- i.e., The form of Hankel matrix is:
.
- A hankel matrix is also called as catalecticant matrix.
- A Hankel matrix is an upside-down Toeplitz matrix.
- A matrix whose entries along a parallel to the main anti-diagonal are equal, for each parallel.
- Sometimes this type of matrices are also called as orthosymmetric matrices.
Examples
- 1.MATRIX("hankel") = 0.312783548142761
- 2.MATRIX("hankel",3)
| 0.6414852568414062 | 0.9679132911842316 | 0.6076015164144337 |
| 0.9679132911842316 | 0.6076015164144337 | 0.6414852568414062 |
| 0.6076015164144337 | 0.6414852568414062 | 0.9679132911842316 |
- 3.MATRIX("hankel",5,1..10)
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 | 6 |
| 3 | 4 | 5 | 6 | 7 |
| 4 | 5 | 6 | 7 | 8 |
| 5 | 6 | 7 | 8 | 9 |
- 4.MATRIX("hankel",5,-10..0)
| -10 | -9 | -8 | -7 | -6 |
| -9 | -8 | -7 | -6 | -5 |
| -8 | -7 | -6 | -5 | -4 |
| -7 | -6 | -5 | -4 | -3 |
| -6 | -5 | -4 | -3 | -2 |
- 5.MATRIX("hankel",4,["rice","water"])
| rice | water | rice | water |
| water | rice | water | rice |
| rice | water | rice | water |
| water | rice | water | rice |
- 6. MATRIX("hankel:integer")
-8
- 7.MATRIX("hankel:positive integer")
61
- 8.MATRIX("hankel:negative integer")
-73
Related Videos
See Also
References
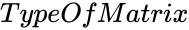 is the type of the matrix.
is the type of the matrix.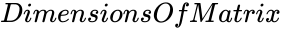 is the order of the Hankel matrix.
is the order of the Hankel matrix.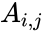 , then we have
, then we have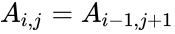 .
.
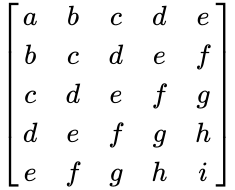 .
.