Difference between revisions of "Manuals/calci/TRIDIAGONAL"
Jump to navigation
Jump to search
| (8 intermediate revisions by 2 users not shown) | |||
| Line 9: | Line 9: | ||
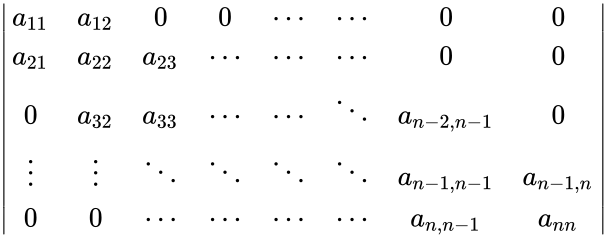
*A tridiagonal is of the form: | *A tridiagonal is of the form: | ||
<math>\begin{vmatrix} | <math>\begin{vmatrix} | ||
| − | a_{11} & a_{12} & 0 & 0 & \cdots & 0 & 0 \\ | + | a_{11} & a_{12} & 0 & 0 & \cdots & \cdots & 0 & 0 \\ |
| − | a_{21} & a_{22} & a_{23} & \cdots & 0 & 0 \\ | + | a_{21} & a_{22} & a_{23} &\cdots & \cdots & \cdots & 0 & 0 \\ |
| − | 0 & a_{32} & a_{33} & \ddots & a_{n-2,n-1} & 0 \\ | + | 0 & a_{32} & a_{33} & \cdots & \cdots &\ddots & a_{n-2,n-1} & 0 \\ |
| − | \vdots &\ddots & \ddots & \ddots & a_{n-1,n-1} & a_{n-1,n} | + | \vdots &\vdots &\ddots &\ddots & \ddots & \ddots & a_{n-1,n-1} & a_{n-1,n}\\ |
| − | 0 & 0 & \cdots &\cdots & a_{n,n-1} & a_{nn} | + | 0 & 0 & \cdots &\cdots &\cdots & \cdots & a_{n,n-1} & a_{nn}\\ |
\end{vmatrix}</math> | \end{vmatrix}</math> | ||
*A general tridiagonal matrix is not necessarily symmetric or Hermitian,but tridiagonal matrix is a matrix that is both upper and lower Hessenberg matrix. | *A general tridiagonal matrix is not necessarily symmetric or Hermitian,but tridiagonal matrix is a matrix that is both upper and lower Hessenberg matrix. | ||
*In Calci, MATRIX("tridiagonal") gives the tridiagonal matirx of order 3. | *In Calci, MATRIX("tridiagonal") gives the tridiagonal matirx of order 3. | ||
*Users can change the order of the matrix. | *Users can change the order of the matrix. | ||
| + | |||
| + | |||
| + | ==Examples== | ||
| + | *MATRIX("tridiagonal") =18 | ||
| + | *MATRIX("tridiagonal",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 59 || 58 || 0 | ||
| + | |- | ||
| + | | -93 || 3 || 21 | ||
| + | |- | ||
| + | | 0 || -24 || 90 | ||
| + | |} | ||
| + | *MATRIX("tridiagonal",6) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 23 || 9 || 0 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | -6 || 91 || -75 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 32 || -25 || -11 || 0 || 0 | ||
| + | |- | ||
| + | |0 || 0 || -44 || 42 || -1 || 0 | ||
| + | |- | ||
| + | |0 || 0 || 0 || 61 || -26 || 86 | ||
| + | |- | ||
| + | |0 || 0 || 0 || 0 || -50 || -92 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|fqn0nW-WXTs|280|center|Tridiagonal Matix}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/BIDIAGONAL| BIDIAGONAL]] | ||
| + | *[[Manuals/calci/PENTADIAGONAL| PENTADIAGONAL]] | ||
| + | *[[Manuals/calci/TRIANGULAR| TRIANGULAR]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://mathworld.wolfram.com/TridiagonalMatrix.html Tridiagonal Matrix] | ||
Latest revision as of 01:45, 26 October 2015
MATRIX("TRIDIAGONAL",order)
- is the size of the Tridiagonal matrix.
Description
- This function returns the matrix with the property of tridiagonal.
- A square matrix with nonzero elements only on the diagonal and slots horizontally or vertically adjacent the diagonal.
- i.e., along the subdiagonal and superdiagonal.
- So a tridiagonal matrix is a matrix that has nonzero elements only on the main diagonal, the first diagonal below this, and the first diagonal above the main diagonal.
- A tridiagonal is of the form:
- A general tridiagonal matrix is not necessarily symmetric or Hermitian,but tridiagonal matrix is a matrix that is both upper and lower Hessenberg matrix.
- In Calci, MATRIX("tridiagonal") gives the tridiagonal matirx of order 3.
- Users can change the order of the matrix.
Examples
- MATRIX("tridiagonal") =18
- MATRIX("tridiagonal",3)
| 59 | 58 | 0 |
| -93 | 3 | 21 |
| 0 | -24 | 90 |
- MATRIX("tridiagonal",6)
| 23 | 9 | 0 | 0 | 0 | 0 |
| -6 | 91 | -75 | 0 | 0 | 0 |
| 0 | 32 | -25 | -11 | 0 | 0 |
| 0 | 0 | -44 | 42 | -1 | 0 |
| 0 | 0 | 0 | 61 | -26 | 86 |
| 0 | 0 | 0 | 0 | -50 | -92 |
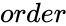 is the size of the Tridiagonal matrix.
is the size of the Tridiagonal matrix.