Difference between revisions of "Manuals/calci/IPMT"
Jump to navigation
Jump to search
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IPMT( | + | <div style="font-size:30px">'''IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)'''</div><br/> |
| − | *<math> | + | *<math>Rate</math> is the annual rate of interest. |
| − | *<math> | + | *<math>Period</math> is the period of to find the interest rate. |
| − | *<math> | + | *<math>NoPaymentPeriods</math> is the number of installments. |
| − | *<math> | + | *<math>PresentValue</math> is the present value. |
| − | *<math> | + | *<math>FutureValue</math> is the future value. |
*<math>Type</math> is either 1 or 0. | *<math>Type</math> is either 1 or 0. | ||
| + | **IPMT(), returns the interest payment for an investment for a given period. | ||
==Description== | ==Description== | ||
*This function gives amount of interest for a particular time, according to the periodic, fixed payments and fixed interest rate. | *This function gives amount of interest for a particular time, according to the periodic, fixed payments and fixed interest rate. | ||
*This function can be used to calculate the payments for a loan or the future value of an investment. | *This function can be used to calculate the payments for a loan or the future value of an investment. | ||
| − | *In <math>IPMT( | + | *In <math>IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)</math>, where <math>Rate</math> is the rate of interest for a year |
| − | *<math> | + | *<math>Period</math> is the period for which the interest payment is to be calculated. It must be a value between <math>1</math> and <math>NoPaymentPeriods</math>. |
| − | *<math> | + | *<math>NoPaymentPeriods</math> is the total number of periods over which the loan or investment is to be paid. |
| − | *<math> | + | *<math>PresentValue</math> is the present value of the loan. |
| − | *<math> | + | *<math>FutureValue</math> is the future value of the loan, at the end of <math>NoPaymentPeriods</math> payment. |
*<math>Type</math> is the number <math>0</math> or <math>1</math>. | *<math>Type</math> is the number <math>0</math> or <math>1</math>. | ||
*When type value is <math>0</math> means the payment is made at the end of the period and type value is <math>1</math> means the payment is made at the beginning of the period | *When type value is <math>0</math> means the payment is made at the end of the period and type value is <math>1</math> means the payment is made at the beginning of the period | ||
| − | *Here the arguments <math> | + | *Here the arguments <math>FutureValue</math> and <math>Type</math> are optional. |
| − | *Suppose we omit the value of <math> | + | *Suppose we omit the value of <math>FutureValue</math>, then it will consider the value as <math>0</math>. |
*Also when we are not giving the <math>Type</math> value, the default value is <math>0</math>. | *Also when we are not giving the <math>Type</math> value, the default value is <math>0</math>. | ||
| − | *Suppose we calculate the monthly payments instead of annual payment, for the argument <math> | + | *Suppose we calculate the monthly payments instead of annual payment, for the argument <math>Rate</math> we have to divide by <math>12</math> and the <math>np</math> value we have multiply with <math>12</math>. |
| − | *For e.g. The monthly payments on a 5 year loan at 10% annual interest, we have to give the arguments <math> | + | *For e.g. The monthly payments on a 5 year loan at 10% annual interest, we have to give the arguments <math>Rate</math> and <math>NoPaymentPeriods</math> as 10%/12 for <math>Rate</math> and 5*12 for <math>NoPaymentPeriods</math>. |
*This function will give result as error when | *This function will give result as error when | ||
Any one of the argument is non-numeric | Any one of the argument is non-numeric | ||
| − | <math> | + | <math>Period < 0</math> or <math>period > NoPaymentPeriods</math> |
==ZOS== | ==ZOS== | ||
| − | *The syntax is to calculate amount of interest for a particular time in ZOS is <math>IPMT( | + | *The syntax is to calculate amount of interest for a particular time in ZOS is |
| − | **<math> | + | <math>IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)</math> |
| − | **<math> | + | **<math>Rate</math> is the annual rate of interest. |
| − | **<math> | + | **<math>Periods</math> is the period of to find the interest rate. |
| − | **<math> | + | **<math>NoPaymentPeriods</math> is the number of installments. |
| − | **<math> | + | **<math>PresentValue</math> is the present value. |
| + | **<math>FutureValue</math> is the future value. | ||
**<math>Type</math> is either 1 or 0. | **<math>Type</math> is either 1 or 0. | ||
*For e.g., | *For e.g., | ||
| Line 56: | Line 58: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] | [http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:34, 29 June 2018
IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)
- is the annual rate of interest.
- is the period of to find the interest rate.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NoPaymentPeriods} is the number of installments.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PresentValue} is the present value.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle FutureValue} is the future value.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Type}
is either 1 or 0.
- IPMT(), returns the interest payment for an investment for a given period.
Description
- This function gives amount of interest for a particular time, according to the periodic, fixed payments and fixed interest rate.
- This function can be used to calculate the payments for a loan or the future value of an investment.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Rate} is the rate of interest for a year
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Period} is the period for which the interest payment is to be calculated. It must be a value between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NoPaymentPeriods} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NoPaymentPeriods} is the total number of periods over which the loan or investment is to be paid.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PresentValue} is the present value of the loan.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle FutureValue} is the future value of the loan, at the end of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NoPaymentPeriods} payment.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Type} is the number Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} .
- When type value is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} means the payment is made at the end of the period and type value is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} means the payment is made at the beginning of the period
- Here the arguments Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle FutureValue} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Type} are optional.
- Suppose we omit the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle FutureValue} , then it will consider the value as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} .
- Also when we are not giving the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Type} value, the default value is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} .
- Suppose we calculate the monthly payments instead of annual payment, for the argument Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Rate} we have to divide by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 12} and the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle np} value we have multiply with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 12} .
- For e.g. The monthly payments on a 5 year loan at 10% annual interest, we have to give the arguments Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Rate} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NoPaymentPeriods} as 10%/12 for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Rate} and 5*12 for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NoPaymentPeriods} .
- This function will give result as error when
Any one of the argument is non-numeric
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Period < 0}
or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle period > NoPaymentPeriods}
ZOS
- The syntax is to calculate amount of interest for a particular time in ZOS is
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IPMT (Rate,Period,NoPaymentPeriods,PresentValue,FutureValue,Type)}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Rate} is the annual rate of interest.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Periods} is the period of to find the interest rate.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NoPaymentPeriods} is the number of installments.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PresentValue} is the present value.
- is the future value.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Type} is either 1 or 0.
- For e.g.,
Examples
- 1.Calculate the interest payment during half yearly 1 and 2 of a loan for 50,000, that is to be reduced to 10,000 over a period of 3 years, by a series of constant half-yearly payments.
- Interest is charged at a rate of 4.5% per year and the payment is made at the beginning of each half year.
- IPMT(4.5%/2,3,2*2,50000,10000,1)= -454.78404196736113
- 2.The interest payment for a $55000 investment that earns 7.50% annually for 15 years.
- The interest payment is calculated for the 5th year and payments are due at the end of each year.
IPMT(7.5%/1, 5, 15*1, 55000)=-3418.570
Related Videos
See Also
References
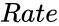 is the annual rate of interest.
is the annual rate of interest.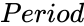 is the period of to find the interest rate.
is the period of to find the interest rate.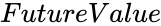 is the future value.
is the future value.