Difference between revisions of "Manuals/calci/IMLOG"
Jump to navigation
Jump to search
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''IMLOG (ComplexNumber,Base)'''</div><br/> | <div style="font-size:30px">'''IMLOG (ComplexNumber,Base)'''</div><br/> | ||
| − | *<math>ComplexNumber</math> is any complex number. | + | *<math>ComplexNumber</math> is any complex number of the form x+iy. |
*<math>Base</math> is the base value of the Log. | *<math>Base</math> is the base value of the Log. | ||
| + | **IMLOG(),returns the logarithm of a complex number to the given base. | ||
==Description== | ==Description== | ||
| Line 22: | Line 23: | ||
# IMLOG("54",5) =2.4784951415313494+ⅈ0 | # IMLOG("54",5) =2.4784951415313494+ⅈ0 | ||
# IMLOG("-19i",9) = 1.3400719296231876-ⅈ0.7149002168450317 | # IMLOG("-19i",9) = 1.3400719296231876-ⅈ0.7149002168450317 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=mO-K8ZCdvfQ|280|center|Complex Logarithm}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 15:06, 22 February 2019
IMLOG (ComplexNumber,Base)
- is any complex number of the form x+iy.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Base}
is the base value of the Log.
- IMLOG(),returns the logarithm of a complex number to the given base.
Description
- This function shows the log value of a complex number.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle IMLOG (ComplexNumber,Base)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ComplexNumber} is any complex number.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Base} is the base value of a Log values.
- A complex logarithm function is an "inverse" of the complex exponential function.
- It is same as the real natural logarithm ln x is the inverse of the real exponential function.
- Thus, a logarithm of a complex number z is a complex number w such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^w = z} .
- The notation for such a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w} is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ln z} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle log z} .
- If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = re^{i\theta}} with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r > 0} which is in Polar form, then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w = ln r + i\theta} is one logarithm of z.
- Adding integer multiples of 2πi gives all the others.
- The complex exponential function is not injective, because Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{w+2\pi i} = e^w} for any w, since adding iθ to w has the effect of rotating Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^w} counterclockwise θ radians.
- So the points Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle .....w-4\pi i,w-2 \pi i, w, w+2\pi i,w+4 \pi i....}
Examples
- IMLOG("2+3i",2) = 1.850219859070546+ⅈ1.417871630745722
- IMLOG("9-5i",3) = 2.122422597222964-ⅈ0.4615809504617068
- IMLOG("9-5i",6) = 1.3013574573492332-ⅈ0.2830170640096076
- IMLOG("54",5) =2.4784951415313494+ⅈ0
- IMLOG("-19i",9) = 1.3400719296231876-ⅈ0.7149002168450317
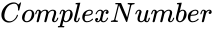 is any complex number of the form x+iy.
is any complex number of the form x+iy.