Difference between revisions of "Manuals/calci/MOPWITHMOD"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
*The syntax is to calculate remainder of the given numbers in ZOS is <math>MOD(Number,Divisor)</math>. | *The syntax is to calculate remainder of the given numbers in ZOS is <math>MOD(Number,Divisor)</math>. | ||
**<math>Number</math> and <math>Divisor</math> are any real numbers. | **<math>Number</math> and <math>Divisor</math> are any real numbers. | ||
| − | *For e.g., | + | *For e.g.,MOD(10,2),MOD(50.2,-4) |
==Examples== | ==Examples== | ||
| Line 26: | Line 26: | ||
#=MOD(-52,7)=4 | #=MOD(-52,7)=4 | ||
#=MOD(0,9)=0 | #=MOD(0,9)=0 | ||
| − | #=MOD(9,0)= | + | #=MOD(9,0)=#N/A (DIVISOR == 0) |
#=MOD(5.5,2)=1.5 | #=MOD(5.5,2)=1.5 | ||
Latest revision as of 03:35, 9 June 2020
MOD(Number,Divisor)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Divisor}
are any real numbers.
- MOD() returns the remainder from division.
Description
- This function gives the remainder of the number after dividing with some number.
- When we divide two integers we will get the result like this: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{X}{Y}= Q} with remainder Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} . Here Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X } is the dividend, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} is the divisor, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} is the Quotient and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} is the remainder.So Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MOD(n,d)=R} .
- For e.g., MOD(5,2)=1. Here 1 is the remainder.
- Ler number be "n" and the divisor be "d"
- The Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MOD} function we can write using Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle INT} function: .
- This function will return the result as error when the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} value is 0.
- Suppose the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} with same sign either '+' or '-',then the result also with same sign.
- But Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} are with different then the result will come with the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d } sign only.
ZOS
- The syntax is to calculate remainder of the given numbers in ZOS is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MOD(Number,Divisor)}
.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Number} and are any real numbers.
- For e.g.,MOD(10,2),MOD(50.2,-4)
Examples
- =MOD(7,2)=1
- =MOD(-19,-3)=-1
- =MOD(75,5)=0
- =MOD(12,-4)=0
- =MOD(85,-9)=-5
- =MOD(-52,7)=4
- =MOD(0,9)=0
- =MOD(9,0)=#N/A (DIVISOR == 0)
- =MOD(5.5,2)=1.5
Related Videos
See Also
References
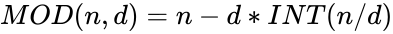 .
.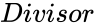 are any real numbers.
are any real numbers.