Difference between revisions of "Manuals/calci/WEIBULL"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font color="#484848"><font face="Arial, sans-serif"><font size="2">'''WEIBULL'''</font></font></font><font color="#4...") |
|||
| (13 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''WEIBULL (Number,Alpha,Beta,Cumulative) '''</div><br/> |
| + | *<math>Number </math> is the value of the function. | ||
| + | *<math>Alpha </math> and <math> Beta </math> are the parameter of the distribution. | ||
| + | *<math>Cumulative</math> is the logical value. | ||
| + | **WEIBULL(),returns the Weibull distribution. | ||
| − | + | ==Description== | |
| + | *This function gives the value of the weibull distribution with 2-parameters. | ||
| + | *It is a continuous probability distribution. | ||
| + | *Weibull distribution also called Rosin Rammler distribution. | ||
| + | *It is used to model the lifetime of technical devices and is used to describe the particle size distribution of particles generated by grinding, milling and crushing operations. | ||
| + | *This distribution is closely related to the lognormal distribution. | ||
| + | *In <math>WEIBULL(Number,Alpha,Beta,Cumulative)</math>,<math> Number </math> is the value to evaluate the function. | ||
| + | *<math> Alpha </math> is the shape parameter of the distribution.<math> Beta </math> is the scale parameter of the distribution. | ||
| + | *<math>Cumulative</math> is the logical value which determines the form of the distribution. | ||
| + | *When <math>Cumulative</math> is TRUE, this function gives the value of the cumulative distribution. When <math>Cumulative</math> is FALSE, then this function gives the value of the probability density function. | ||
| + | *When we are not omitting the value of <math>Cumulative</math>, then it consider as FALSE. | ||
| + | *Weibull distribution is of two type :3-parameter weibull distribution and 2-parameter weibull distribution. | ||
| + | *This function gives the value of 2-parameter weibull distribution by setting the third parameter (location parameter) is zero. | ||
| + | *Also if alpha<1,then the failure rate of the device decreases over time. | ||
| + | *If alpha=1, then the failure rate of the device is constant over time. | ||
| + | *If alpha>1, then the failure rate of the device increases over time. | ||
| + | *The equation for cumulative distribution function is: <math>F(x,\alpha,\beta)</math> =<math>1-e^-{(\frac{x}{\beta})}^\alpha</math>. | ||
| + | *The equation for probability density function is: | ||
| + | <math>f(x,\alpha,\beta) = \frac{\alpha}{\beta^\alpha}.x^{\alpha-1}.e^-{(\frac{x}{\beta})}^\alpha.</math> | ||
| + | *When alpha =1, then this function gives the exponential with <math>\lambda=\frac{1}{\beta}</math>. | ||
| + | *This function gives the result as error when | ||
| + | 1. Any one of the argument is non-numeric. | ||
| + | 2. Number is negative. | ||
| + | 3. Alpha<math>\le 0</math> or Beta <math>\le 0</math> | ||
| − | + | ==Examples== | |
| + | #=WEIBULL(202,60,81,TRUE) = 1 | ||
| + | #=WEIBULL(202,60,81,FALSE) = 0 | ||
| + | #=WEIBULL(160,80,170,TRUE) = 0.00779805060 | ||
| + | #=WEIBULL(160,80,170,FALSE) = 0.0038837823333 | ||
| + | #= WEIBULL(10.5,2.1,5.3,TRUE) = 0.9850433821261 | ||
| + | #=WEIBULL(10.5,2.1,5.3,FALSE) = 0.0125713406729 | ||
| − | + | ==Related Videos== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{#ev:youtube|mMo0Nvqq3qA|280|center|Weibull Probability}} | |
| − | |||
| − | |||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/EXPONDIST | EXPONDIST ]] | ||
| + | *[[Manuals/calci/LOGNORMDIST | LOGNORMDIST ]] | ||
| − | + | ==References== | |
| + | *[http://en.wikipedia.org/wiki/Weibull_distribution Weibull distribution] | ||
| − | |||
| − | |||
| − | * | + | *[[Z_API_Functions | List of Main Z Functions]] |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 16:32, 10 August 2018
WEIBULL (Number,Alpha,Beta,Cumulative)
- is the value of the function.
- and are the parameter of the distribution.
- is the logical value.
- WEIBULL(),returns the Weibull distribution.
Description
- This function gives the value of the weibull distribution with 2-parameters.
- It is a continuous probability distribution.
- Weibull distribution also called Rosin Rammler distribution.
- It is used to model the lifetime of technical devices and is used to describe the particle size distribution of particles generated by grinding, milling and crushing operations.
- This distribution is closely related to the lognormal distribution.
- In , is the value to evaluate the function.
- is the shape parameter of the distribution.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Beta } is the scale parameter of the distribution.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cumulative} is the logical value which determines the form of the distribution.
- When Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cumulative} is TRUE, this function gives the value of the cumulative distribution. When Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cumulative} is FALSE, then this function gives the value of the probability density function.
- When we are not omitting the value of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cumulative} , then it consider as FALSE.
- Weibull distribution is of two type :3-parameter weibull distribution and 2-parameter weibull distribution.
- This function gives the value of 2-parameter weibull distribution by setting the third parameter (location parameter) is zero.
- Also if alpha<1,then the failure rate of the device decreases over time.
- If alpha=1, then the failure rate of the device is constant over time.
- If alpha>1, then the failure rate of the device increases over time.
- The equation for cumulative distribution function is: =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-e^-{(\frac{x}{\beta})}^\alpha} .
- The equation for probability density function is:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x,\alpha,\beta) = \frac{\alpha}{\beta^\alpha}.x^{\alpha-1}.e^-{(\frac{x}{\beta})}^\alpha.}
- When alpha =1, then this function gives the exponential with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\frac{1}{\beta}} .
- This function gives the result as error when
1. Any one of the argument is non-numeric.
2. Number is negative.
3. AlphaFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \le 0}
or Beta Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \le 0}
Examples
- =WEIBULL(202,60,81,TRUE) = 1
- =WEIBULL(202,60,81,FALSE) = 0
- =WEIBULL(160,80,170,TRUE) = 0.00779805060
- =WEIBULL(160,80,170,FALSE) = 0.0038837823333
- = WEIBULL(10.5,2.1,5.3,TRUE) = 0.9850433821261
- =WEIBULL(10.5,2.1,5.3,FALSE) = 0.0125713406729
Related Videos
See Also
References
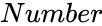 is the value of the function.
is the value of the function.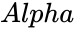 and
and 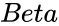 are the parameter of the distribution.
are the parameter of the distribution.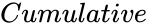 is the logical value.
is the logical value.
 ,
,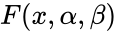 =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-e^-{(\frac{x}{\beta})}^\alpha}
.
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-e^-{(\frac{x}{\beta})}^\alpha}
.