Difference between revisions of "Manuals/calci/EXP"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
*It can calculate the sum of infinite series: <math>e=1+(1/1)+(1/1.2)+(1/1.2.3)+(1/1.2.3.4) +...</math> | *It can calculate the sum of infinite series: <math>e=1+(1/1)+(1/1.2)+(1/1.2.3)+(1/1.2.3.4) +...</math> | ||
*And the inverse function of the natural logarithm function is the exponential function: | *And the inverse function of the natural logarithm function is the exponential function: | ||
| − | + | <math>f^{-1}(x) = e^x</math>. | |
==Examples== | ==Examples== | ||
Revision as of 06:10, 21 November 2013
EXP(x)
- where is the number .
Description
- This function gives the raised to the power of number.
- In , where represents the exponent of , or .
- The approximate value of the constant and it is equal to or .
- It is called the Mathematical Constant or Euler's Number or Napier's Constant.
- It is the base of natural logarithm.
- It can calculate the sum of infinite series:
- And the inverse function of the natural logarithm function is the exponential function:
.
Examples
- EXP(1)=2.718281828459045
- EXP(0)=1
- EXP(-5)=0.0067379469990
- EXP(6.3)=544.5719101259
 is the number .
is the number .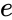 raised to the power of number.
raised to the power of number.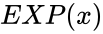 , where
, where 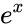 .
.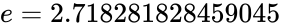 and it is equal to
and it is equal to 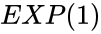 .
.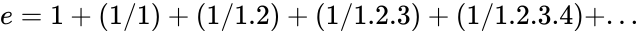
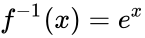 .
.