Manuals/calci/IMEXP
Jump to navigation
Jump to search
IMEXP(ComplexNumber)
- is of the form x+iy.
- IMEXP(), returns the exponential of a complex number.
Description
- This function gives the exponential of a complex number.
- In , is of the form , & are real numbers & is the imaginary unit. .
- Euler's formula states that , for any real number and is the base of the natural logarithm.
- The approximate value of the constant e=2.718281828459045 and it is equal to .
- Let z be the Complex Number.Then the exponential of a complex number is : .
- Here Sin and Cos are trignometric functions. y is angle value in radians.
- When imaginary part is '0', it will give the exponent value of the real number. i.e when imaginary number is '0'.
- The Complex exponential function is denoted by "cis(x)"(Cosine plus iSine)
- We can use COMPLEX function to convert the real and imaginary coefficients to a complex number.
ZOS
- The syntax is to calculate IMEXP in ZOS is .
- is of the form a+bi.
- For e.g.,IMEXP("0.3-0.54i")
Examples
- =IMEXP("2+3i") = -7.315110094901102+1.0427436562359i
- =IMEXP("4-5i") = 15.4874305606508+52.355491418482i
- =IMEXP("6") = 403.428793492735+0i
- =IMEXP("2i") = -0.416146836547142+0.909297426825682i
- =IMEXP("0") = 1+0i and IMEXP("0i") = 1+0i
Related Videos
See Also
References
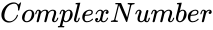 is of the form x+iy.
is of the form x+iy.
 ,
, 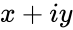 ,
,  &
&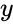 are real numbers &
are real numbers &  is the imaginary unit.
is the imaginary unit. 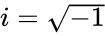 .
. , for any real number
, for any real number 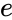 is the base of the natural logarithm.
is the base of the natural logarithm.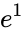 .
.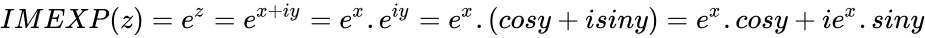 .
.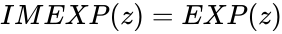 when imaginary number
when imaginary number 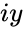 is '0'.
is '0'.