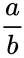Difference between revisions of "Manuals/calci/GOLDENRATIO"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. | *Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. | ||
| − | *Golden ratio is represented as '''phi(φ)''' and its conjugate is represented as '''Phi (&Phi)'''. | + | *Golden ratio is represented as '''phi(φ also called smallphi)''' and its conjugate is represented as '''Phi (Φ also called capitalphi)'''. |
*If 'a' and 'b' are two quantities with 'a>b', then | *If 'a' and 'b' are two quantities with 'a>b', then | ||
| − | + | φ = <math>\frac{(a + b)}{a}</math> = <math>\frac {a}{b}</math> | |
*Using quadratic formula, golden ratio is represented as - | *Using quadratic formula, golden ratio is represented as - | ||
| − | φ = <math>\frac{1+& | + | φ = <math>\frac{(1 + √5)}{2}</math> = 1.618033988749895 |
| − | Φ = <math>\frac{1-& | + | Φ = <math>\frac{(1 - √5)}{2}</math> = -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi. |
*Argument <math>phismall</math> can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1. | *Argument <math>phismall</math> can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1. | ||
Revision as of 07:38, 19 December 2013
GOLDENRATIO(phismall)
- where is the logical value TRUE or FALSE.
GOLDENRATIO() returns the golden ratio value.
Description
- Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities.
- Golden ratio is represented as phi(φ also called smallphi) and its conjugate is represented as Phi (Φ also called capitalphi).
- If 'a' and 'b' are two quantities with 'a>b', then
φ = =
- Using quadratic formula, golden ratio is represented as -
φ = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{(1 + √5)}{2}}
= 1.618033988749895
Φ = Failed to parse (syntax error): {\displaystyle \frac{(1 - √5)}{2}}
= -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi.
- Argument can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1.
- If argument is omitted, Calci assumes it as TRUE or 1 and displays the output as 0.6180339887498948.
- If argument is invalid, Calci returns a #NULL error message.
Examples
GOLDENRATIO(TRUE) returns 0.6180339887498948, value of capitalphi Φ
GOLDENRATIO(1) returns 0.6180339887498948, value of capitalphi Φ
GOLDENRATIO(FALSE) returns 1.618033988749895, value of smallphi φ
GOLDENRATIO() returns 0.6180339887498948, value of capitalphi Φ
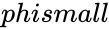 is the logical value TRUE or FALSE.
is the logical value TRUE or FALSE.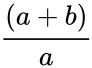 =
=