Difference between revisions of "Manuals/calci/MINVERSE"
Jump to navigation
Jump to search
| Line 25: | Line 25: | ||
*Where <math>adj(A)</math> is the adjoint of <math>A</math>. | *Where <math>adj(A)</math> is the adjoint of <math>A</math>. | ||
*Adjoint is the matrix formed by taking the Transpose of the Co-factor matrix of the original matrix. | *Adjoint is the matrix formed by taking the Transpose of the Co-factor matrix of the original matrix. | ||
| − | *Also <math>A.A^-1=A^-1.A=I</math>, where <math>I</math> is the identity matrix. | + | *Also <math>A.A^{-1}=A^{-1}.A = I</math>, where <math>I</math> is the identity matrix. |
*Non-square matrices do not have inverses. | *Non-square matrices do not have inverses. | ||
*Not all square matrices have inverses. | *Not all square matrices have inverses. | ||
Revision as of 05:08, 1 January 2014
MINVERSE(arr)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arr} is the array of numeric elements
Description
- This function gives the inverse matrix for the given matrix.
- We have to find a inverse of a matrix then it should satisfy the following conditions
- 1.A matrix must be a square matrix.
- 2.It's determinant not equal to 0.
- Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} be the 2x2 matrix with the elements
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}} .
- Then the inverse of matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is denoted by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{-1}} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{-1}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}^{-1}= \frac{1}{ad-bc} * \begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix} }
- Now let be the matrix is of order Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle nXn} .
- Then the inverse of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{-1}= \frac{1}{det(A)}*adj(A)}
- Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle adj(A)} is the adjoint of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} .
- Adjoint is the matrix formed by taking the Transpose of the Co-factor matrix of the original matrix.
- Also Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A.A^{-1}=A^{-1}.A = I} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} is the identity matrix.
- Non-square matrices do not have inverses.
- Not all square matrices have inverses.
- A square matrix which has an inverse is called invertible or non-singular, and a square matrix without an inverse is called non-invertible or singular.
- This function will return the result as error when
1. Any one of the cell is non-numeric or any cell is empty or contain text 2. Suppose number of rows not equal to number of columns
Examples
Matrix A A=(4 3
3 2)
MINVERSE(B5:C6)=(-2 3
3 -4)
MATRIX A A=(3 4
6 8)
MINVERSE(C4:D5)=Null, because its det value is 0. MATRIX A A=(2 3
4 7)
MINVERSE(B4:C5)=(3.5 -1.5
-2 1)
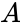 be the matrix is of order Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle nXn}
.
be the matrix is of order Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle nXn}
.