Difference between revisions of "Manuals/calci/MOODSMEDIANTEST"
Jump to navigation
Jump to search
| Line 20: | Line 20: | ||
*The test interpretation is: | *The test interpretation is: | ||
*Null hypothesis<math>(H_0)</math>:The population medians all are equal.Alternative hypothesis<math>(H_a)</math>:Atleast one of the medians is different from another. | *Null hypothesis<math>(H_0)</math>:The population medians all are equal.Alternative hypothesis<math>(H_a)</math>:Atleast one of the medians is different from another. | ||
| − | *If the null hypothesis is true, any given observation will have probability 0.5 of being greater than the shared median. *For each sample,the number of observations greater than the shared median would have a binomial distribution with p = 0.5*'''The procedure of the test is''': | + | *If the null hypothesis is true, any given observation will have probability 0.5 of being greater than the shared median. *For each sample,the number of observations greater than the shared median would have a binomial distribution with p=0.5 |
| + | *'''The procedure of the test is''': | ||
*1. Determine the overall median. | *1. Determine the overall median. | ||
*The combined data from all groups are sorted and the median is calculated: | *The combined data from all groups are sorted and the median is calculated: | ||
| − | <math>md=\frac{(x_{\frac{n}{2}}+x_{(\frac{n}{2}+1)})}{2}</math>,if n is even. | + | :<math>md=\frac{(x_({\frac{n}{2})}+x_{(\frac{n}{2}+1)})}{2}</math>,if n is even. |
| + | :<math>md=x_(\frac{(n+1)}{2})</math>,if n is odd. | ||
*2. For each sample, count how many observations are greater than the overall median, and how many are equal to or less than it. | *2. For each sample, count how many observations are greater than the overall median, and how many are equal to or less than it. | ||
*3. Put the counts from step 2 into a 2xk contingency table: | *3. Put the counts from step 2 into a 2xk contingency table: | ||
*4. Perform a chi-square test on this table, testing the hypothesis that the probability of an observation being greater than the overall median is the same for all populations. | *4. Perform a chi-square test on this table, testing the hypothesis that the probability of an observation being greater than the overall median is the same for all populations. | ||
Revision as of 22:46, 21 May 2014
MOODSMEDIANTEST(xRange,yRange,Confidencelevel,Logicalvalue)
- is the array of x values.
- is the array of y values.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the test statistic of the Mood's median test.
- It is one of the Non parametric test.
- This function is used to test the equality of medians from two or more populations.
- So it provides a nonparametric alternative to the one way ANOVA.
- It is a special case of Pearson's chi-squared test.
- This function works when the Y variable is continuous,discrete-ordinal or discrete -count,and the X variable is discrete with two or more attributes.
- This test does not require normally distributed data,which is does not mean that it is assumption free.
- The following assumptions are required to test this function:
- 1.Sample data drawn from the populations of interest are unbiased and representative.
- 2.Data of k populations are continuous or ordinal when the spacing between adjacent values is not constant.
- 3.k populations are independent from each other.
- 4.The distributions of the populations the samples were drawn from all have the same shape.
- The test interpretation is:
- Null hypothesis:The population medians all are equal.Alternative hypothesis:Atleast one of the medians is different from another.
- If the null hypothesis is true, any given observation will have probability 0.5 of being greater than the shared median. *For each sample,the number of observations greater than the shared median would have a binomial distribution with p=0.5
- The procedure of the test is:
- 1. Determine the overall median.
- The combined data from all groups are sorted and the median is calculated:
- ,if n is even.
- ,if n is odd.
- 2. For each sample, count how many observations are greater than the overall median, and how many are equal to or less than it.
- 3. Put the counts from step 2 into a 2xk contingency table:
- 4. Perform a chi-square test on this table, testing the hypothesis that the probability of an observation being greater than the overall median is the same for all populations.
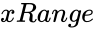 is the array of x values.
is the array of x values.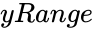 is the array of y values.
is the array of y values.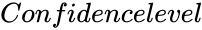 is the value between 0 and 1.
is the value between 0 and 1.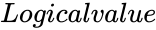 is either TRUE or FALSE.
is either TRUE or FALSE.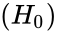 :The population medians all are equal.Alternative hypothesis
:The population medians all are equal.Alternative hypothesis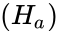 :Atleast one of the medians is different from another.
:Atleast one of the medians is different from another.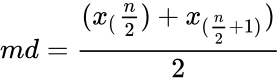 ,if n is even.
,if n is even.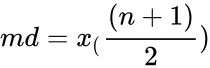 ,if n is odd.
,if n is odd.