Manuals/calci/MOODSMEDIANTEST
Jump to navigation
Jump to search
MOODSMEDIANTEST (XRange1,XRange2,ConfidenceLevel,NewTableFlag)
- is the array of values.
- is the array of values.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the test statistic of the Mood's median test.
- It is one of the Non parametric test.
- This function is used to test the equality of medians from two or more populations.
- So it provides a nonparametric alternative to the one way ANOVA.
- It is a special case of Pearson's chi-squared test.
- This function works when the Y variable is continuous,discrete-ordinal or discrete -count,and the X variable is discrete with two or more attributes.
- This test does not require normally distributed data,which is does not mean that it is assumption free.
- The following assumptions are required to test this function:
- 1.Sample data drawn from the populations of interest are unbiased and representative.
- 2.Data of k populations are continuous or ordinal when the spacing between adjacent values is not constant.
- 3.k populations are independent from each other.
- 4.The distributions of the populations the samples were drawn from all have the same shape.
- The test interpretation is:
- Null hypothesis:The population medians all are equal.Alternative hypothesis:Atleast one of the medians is different from another.
- If the null hypothesis is true, any given observation will have probability 0.5 of being greater than the shared median.
- For each sample,the number of observations greater than the shared median would have a binomial distribution with p=0.5
- The procedure of the test is:
- 1. Determine the overall median.
- The combined data from all groups are sorted and the median is calculated:
- ,if n is even.
- ,if n is odd.
- where .
- ,is the ordered data of all observations from small to large.
- 2. For each sample, count how many observations are greater than the overall median, and how many are equal to or less than it.
- 3. Put the counts from step 2 into a 2xk contingency table:
- 4. Perform a chi-square test on this table, testing the hypothesis that the probability of an observation being greater than the overall median is the same for all populations.
Example
| A | B | |
|---|---|---|
| 1 | 30 | 32 |
| 2 | 10 | 13 |
| 3 | 22 | 33 |
| 4 | 20 | 26 |
| 5 | 43 | 34 |
- =MOODSMEDIANTEST(A1:A5,B1:B5,0.05,TRUE)
MOODSMEDIANTEST STATISTICS
| MEAN1 | 25 |
| MEDIAN1 | 22 |
| MEAN2 | 27.6 |
| MEDIAN2 | 32 |
| OVERALLMEDIAN | 28 |
| GREATERMEDIAN1 | 2 |
| GREATERMEDIAN2 | 3 |
| LESSEQUALMEDIAN1 | 3 |
| LESSEQUALMEDIAN2 | 2 |
| OBSERVED FREQUENCY |
2 3 3 2 |
| EXPECTED FREQUENCY |
2.5 2.5 2.5 2.5 |
| PVALUE | 0.5270892568655381 |
RESULT AS PVALUE > 0.05, MEDIANS OF THE POPULATIONS FROM WHICH THE TWO SAMPLES ARE DERIVED ARE EQUAL
Related Videos
See Also
References
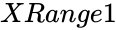 is the array of values.
is the array of values.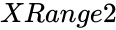 is the array of values.
is the array of values.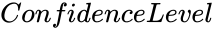 is the value between 0 and 1.
is the value between 0 and 1.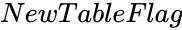 is either TRUE or FALSE.
is either TRUE or FALSE.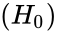 :The population medians all are equal.Alternative hypothesis
:The population medians all are equal.Alternative hypothesis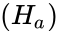 :Atleast one of the medians is different from another.
:Atleast one of the medians is different from another.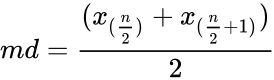 ,if n is even.
,if n is even.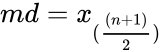 ,if n is odd.
,if n is odd.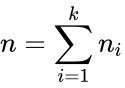 .
.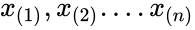 ,is the ordered data of all observations from small to large.
,is the ordered data of all observations from small to large.