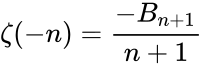Manuals/calci/RIEMANNZETA
Jump to navigation
Jump to search
RIEMANNZETA(s)
- is the value from to .
Description
- This function gives the result for the function of Riemann-Zeta function.
- It is also known as Euler-Riemann Zeta function.
- This function is useful in number theory for the investigating properties of prime numbers.
- It is denoted by .
- This function is defined as the infinite series .
- When the value of s=1,then this series is called the harmonic series.
- When it is increase without any bound or limit, then its sum is infinite.
- When the value of s is larger than 1,the the series converges to a finite number as successive terms are added.
- The riemann zeta function is defined for Complex numbers also.
- So is a function of a complex variable ,where and t are real numbers.i is the imaginary unit.
- It is also a function of a complex variable s that analytically continues the sum of the infinite series , which converges when the real part of s is greater than 1.
- It is defined by : where =Real part of s>1.
- We can define this by integral also:
- Riemann zeta function is a meromorphic function on the whole complex s-plane, which is holomorphic everywhere except for a simple pole at s = 1 with residue 1.
- For special values:
- (i)Any positive integer 2n.
- where is a Bernoulli number.
- (ii)For negative integers:
- For n ≥ 1,so in particular ζ vanishes at the negative even integers because Bm = 0 for all odd m other than 1.
- For odd positive integers, no such simple expression is known.
- When s=1,then ζ (1) is Harmonic series.
- when s=2, then ζ (2) derivation is Basel problem.
- when s=3, then ζ (3) derivation is Apery's constant.
- When s=4, then ζ (4) derivation is Planck's law.
Examples
- =RIEMANNZETA(0)= -1/2
- =RIEMANNZETA(4) = π^4/90
- =RIEMANNZETA(-25)= -657931/12.
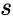 is the value from
is the value from 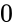 to
to 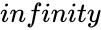 .
.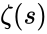 .
.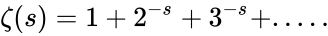 .
.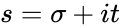 ,where
,where 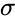 and t are real numbers.i is the imaginary unit.
and t are real numbers.i is the imaginary unit.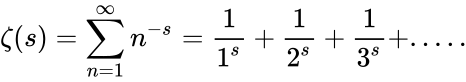 where
where 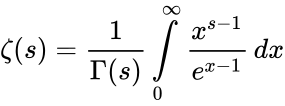
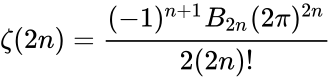 where
where 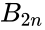 is a Bernoulli number.
is a Bernoulli number.