Difference between revisions of "Manuals/calci/BETAFUNCTION"
Jump to navigation
Jump to search
| Line 14: | Line 14: | ||
#BETAFUNCTION(9.1,7.4) = 0.00001484129272494359 | #BETAFUNCTION(9.1,7.4) = 0.00001484129272494359 | ||
#BETAFUNCTION(876,432) = NaN | #BETAFUNCTION(876,432) = NaN | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=v1uUgTcInQk|280|center|Beta Function}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 15:04, 4 December 2018
BETAFUNCTION (a,b)
- and are any positive real numbers.
Description
- This function returns the value of the Beta function.
- Beta function is also called the Euler integral of the first kind.
- To evaluate the Beta function we usually use the Gamma function.
.
- For x,y positive we define the Beta function by:
Examples
- BETAFUNCTION(10,23) = 1.550093439705759e-9
- BETAFUNCTION(9.1,7.4) = 0.00001484129272494359
- BETAFUNCTION(876,432) = NaN
Related Videos
See Also
References
 and
and 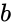 are any positive real numbers.
are any positive real numbers.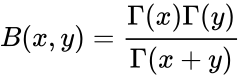 .
.